Forms vs monoidal categories
Below is a summary of the talk given at the Séminaire Itinérant de Catégories (8 October 2021), prepared before the talk. The talk is mainly based on Zurab Janelidze's joint work in progress with Francois van Niekerk, as well as his earlier work on forms with former collaborators.
The talk assumes that the listener is familiar with basic ideas and concepts of category theory found in Categories for the Working Mathematician by Saunders Mac Lane (in particular, Chapters I, VII and VIII), as well as with the notions of factorization system and Grothendieck fibration.
1. Biproducts, products, sums and monoidal categories
The goal of this talk is to explain the following diagram:
Most categories are not linear. Matching of products and sums is a rare phenomenon. So instead of their matching, one looks for a common generalization of these two constructions, especially that there are many other interesting ways of combining objects which one would also want to include under the generalization. The classical example of a construction of combining objects which is neither a product nor a sum is the construction of a tensor product of two abelian groups. A common generalization of these constructions is of course the notion of a monoidal category.
We have thus far described the fragment of the above diagram enclosed in the region shown below:
2. Algebraic vs geometric nature of a category
We will now describe the fragment of the initial diagram enclosed in the region shown below:
The notion of a monoid is equivalent to the notion of a single-object category. So we may think of a monoid as a category with "few objects". What is a category with "few morphisms"? A poset! We may think of a poset as a category in which between any two objects there is at most one morphism (in one or the other direction, to encode antisymmetry as well). So the notion of a category seems to naturally split into two more primitive notions: that of a monoid and that of a poset. This split can be seen as a decomposition of the notion of a category into its algebraic nature (monoid) and its geometric nature (poset). A monoidal category can then be seen as a category enforced with additional algebraic structure. What is then a geometric enforcement of the notion of a category? This is where the notion of a form enters the picture.3. Short exact sequences, subobjects, quotients, and forms
Linearity is an important ingredient of the notion of an abelian category. Another important ingredient is exactness: that every morphism decomposes as a cokernel followed by a kernel. The following result is from "Duality in non-abelian algebra II" by Z. Janelidze and T. Weighill (Journal of Homotopy and Related Structures, 2016):
Let us explain the concepts in this corollary:- A Grandis exact category is a category equipped with an ideal of null morphisms in the sense of C. Ehresmann, such that every morphism admits a decomposition into a cokernel followed by a kernel, relative to the ideal. In the pointed case, this becomes the notion of a Puppe-Mitchell exact category: a pointed category where every morphism decomposes as a cokernel followed by a kernel (both in the usual sense of a pointed category).
- An Isbell bicategory is a category equipped with a proper factorization system. The corresponding "form of quotients" is the fibration of quotients and the "form of subobjects" is the opfibration of subobjects.
Specializing the result above to a pointed category equipped with a proper factorization system given by a class "E" of epimorphisms and class "M" of monomorphisms, we get the following
Theorem: Such a category is exact (i.e., every morphism decomposes as a cokernel followed by a kernel) if and only if the fibration of "E"-quotients is isomorphic to the opfibration of "M"-subobjects.
This theorem is analogous to the fact that a pointed category is linear if and only if it has binary sums and products such that the monoidal structure of sum is isomorphic to the monoidal structure of product. In this analogy, the notion of subobject corresponds to the notion of product and the notion of quotient corresponds to the notion of sum. What corresponds to a monoidal structure is a form, by which we simply mean a faithful functor whose fibres are posets. Both, fibrations of quotients and opfibrations of subobjects are forms. A form equips every object of the category with a poset (the fibre at that object), so in view of the previous discussion about algebraic vs geometric nature of a category, a form can be seen as a geometric enforcement of the notion of a category. There are two canonical types of forms, given by subobject forms and quotient forms, just like there are two canonical types of monoidal structures given by products and sums. Their coincidence, in the context of a pointed category equipped with a proper factorization system, gives, by the above theorem, a characterization of exact categories. On the monoidal side, what corresponds to requiring the existence of a proper factorization is the requirement of the existence of all finite products and sums.
To complete the analogy between the monoidal vs formal situations, we need to answer the following questions:
Question 1. What is geometric/formal analogue of tensor product as a third type of monoidal structure, different from product and sum, but nevertheless an important example of a monoidal structure?
Question 2. What is geometric/formal analogue of the notion of a biproduct?
We leave answering the first question to the end of the talk and answer now the first question. A biproduct is, loosely speaking, something that is both a product and a sum, plus these two must satisfy compatibility conditions. Thus we want something that is both a subobject and a quotient with some compatibility conditions. The answer is: a short exact sequence, i.e., a sequence of morphisms
where the first is a kernel of the second and the second is a cokernel of the first. A linear category can be thought of as a pointed category having sufficiently many biproducts, where "sufficiently many" means that any two objects can be completed to a single biproduct diagram. With some loose analogy, here, an exact category is a pointed category having sufficiently many short exact sequences, where "sufficiently many" means, this time, that any single morphism can be completed to a commutative diagram with two short exact sequences:
To complete description of the diagram, we need to describe its bottom part:4. A Noetherian Form over the Category of Sets
A noetherian form is a form satisfying the axioms given in the paper "Duality in non-abelian algebra IV" by A. Goswami and Z. Janelidze (Advances in Mathematics, 2019). These axioms are self-dual in the sense that a form satisfies them if and only if the dual form (i.e., the dual functor) satisfies them. The axioms allow to establish homomorphism theorems for group-like structures, such as the isomorphism theorems and homological diagram lemmas.
The form of subobjects/quotients of an exact category is noetherian. The form of subobjects of a category having finite limits and colimits is noetherian if and only if it is a semi-abelian category in the sense of G. Janelidze, L. Márki, and W. Tholen (J. Pure Appl. Algebra, 2002). Although neither the category of sets, nor its dual, is a semi-abelian category, it still has a noetherian form. This form is neither a subobject form and nor it is a quotient form. Under this form, the fibre of a set is given by the poset of ordered pairs consisting of an equivalence relation and a subset that is a union of equivalence classes. This form is the (an) answer to Question 1. A thorough analysis of this form is being written up in a joint work of Zurab Janelidze and Francois van Niekerk, which is based on the results given in the PhD Thesis of the second named author.
5. Contrasting Features of the Monoid-Form Analogy
As demonstrated above, there is a striking analogy between the monoidal/formal roots of the notion of an abelian category. This analogy has some interesting contrasting features too:
- A monoidal structure is an internal monoid in the 2-category of categories. A form is not an internal poset in the 2-category of categories.
- Products and sums, once they exist, are unique (up to isomorphism). A category may have several non-isomorphic proper factorization systems.
- Isomorphism between the monoidal structure of product and the monoidal structure of sum forces the category to be pointed. Exact categories need not be pointed categories.
The middle point above could perhaps be remedied by relaxing the notion of a monoidal structure of sum (and accordingly, the dual notion of a monoidal structure of product), replacing it with sum structure in the sense of Z. Janelidze (Cover Relations on Categories, Applied Categorical Structures, 2009): a monoidal structure where the monoidal unit is an initial object and the resulting canonical morphisms into the tensor,
are jointly epimorphic. Isomorphism of a sum structure and a product structure (dual to sum structure) trivially forces pointedness. However, it does not force linearity: this isomorphism holds in every unital category in the sense of D. Bourn. Moreover, a pointed category with products and sums in which the canonical morphism from the coproduct to the product is both a monomorphism and an epimorphism, but not necessarily an isomorphism, will have both the usual sum and the usual product being bisum structures (defined as sum structures which are isomorphic to product structures) without these two being isomorphic to each other. There surely ought to be such a category!
6. Conclusion
An intriguing analogy between the monoidal roots and the formal roots of the notion of an abelian category leads to a new notion of a "bisum structure", which under this analogy presents itself as the counterpart of a Grandis exact structure. Combining these two notions may give an interesting generalization of the notion of an abelian category, not considered yet in the literature. Relaxing a Grandis exact structure to a noetherian form, these ideas will come close to the ideas of Francois van Niekerk developed in "Biproducts and commutators for noetherian forms" (Theory and Applications of Categories, 2019): there he defines a biproduct in the context of a noetherian form, which is an example of our bisum structure.


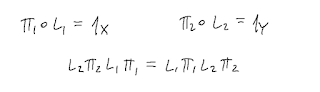








Comments
Post a Comment