Monotony (opus 1128)

The Merriam-Webster Dictionary defines the word "monotony" as "tedious sameness". For a creative soul, monotony is on par with torture. This piece conveys the struggles of the soul that has been trapped in monotony and is looking for ways to break free from it. The video shows a man performing various free style dance moves as an expression of the struggles. Behind him is a wall on which, in the first part of the video, projects a movie of clouds moving through the sky. This is a symbolism of one's creative aspirations before one becomes a prisoner of monotony. In the second part of the video, the projection changes to showing the dancer in action, from multiple angles. This symbolizes that after a while of monotony, the aspirations dissolve into excessive awareness of one's own self. At this stage, an illusion of having broken free from monotony may arise, which is symbolized by the scene with the chair. The chair is the illusion of freedom, illustrated by the dancer performing various dance moves over and around the chair. During the scene with the chair, the music is cheerful. This scene transitions into a scene leading to the finale, where the chair is gone and the mood of the music drops low signifying the sad realization that the feeling of having broken free from monotony was only an illusion. Right at the very end, the scene shows the dancer up close. A moment after the music has stopped, the dancer abruptly turns his head around as part of what seems to be another dance move, which ends the video. It leaves the viewer uncertain whether monotony has been overcome or not; the intention here is to urge the viewer to contemplate on their own monotony and ask the question whether it has been overcome or not?

Read More

A Gap in Mathematics Education

The process of creation of mathematics has the following hierarchically dependent components:

• Coming up with a concept.
• Coming up with a question dealing with a relationship between concepts (this includes formulating a hypothesis, as well as finding an example or a counterexample of a concept/phenomenon).
• Answering a question dealing with a relationship between concepts (this includes proving theorems as well as solving problems without being given the recipe for solution).
• Applying the answer to a question dealing with a relationship between concepts to answer another such question (this includes solving problems by applying a given recipe for solution).

Modern mathematics education (both at the school and at the university levels) focuses mainly on the last two points. What is regarded as a low quality mathematics education would focus only on the last point. For a more whole mathematics education, the first two points must receive as much attention as the last two points do. 

It is not difficult to implement the first two points in the practice of mathematics teaching. Here is an example of the structure of a class that focuses on the second and the third points:

1. The teacher proposes one or two concepts that the pupils are familiar with (perhaps, by taking suggestions from the class). 
2. The teacher then asks the pupils to explain the concepts, helping the pupils in the explanation, when necessary. 
3. Then, the teachers asks the pupils to think of a question that would combine the named concepts. The teacher helps in this process.
4. After this, the teacher and the pupils engage in answering the question together. 
5. If the question is too hard to answer, it should be concretized to a simpler question. If the question is too easy to answer, it should be abstracted to a more difficult question.

Concepts arise in mathematics as a necessity to help one express a general phenomenon. Incorporation of the first point in a classroom can be achieved by explaining this necessity for the concepts that the pupils are already familiar with, or by taking pupils on a journey that would help them identify such a necessity and will result in (re)discovering a mathematical concept. Teaching concepts by first showing examples and then asking the pupil to develop a concept that fits those examples is another, perhaps simpler, way. The activities which ask a pupil to identify a pattern in a sequence of numbers or figures is in some sense of this type. However, these activities are sold as activities that fall under the third point, as the pupil is being convinced that the question must have one definite answer.

Read More

Metaphysics of Human Function based on a Mathematical Structure

work in progress

I propose here a theory of human function, which I have been developing based on introspection. In this theory, human function is represented in terms of exchange of information of four agents, which I call the spirit, the mind, the soul and the body. Although these are surely familiar terms, having a variety of scientific, pseudo-scientific, religious, philosophical and other usage, I do not assume any insight derived from such usage. The essence of each of these agents will be revealed through the roles that they play in human function. Matching of this essence with any of the existing definitions of these entities is unintentional and may well be coincidental.

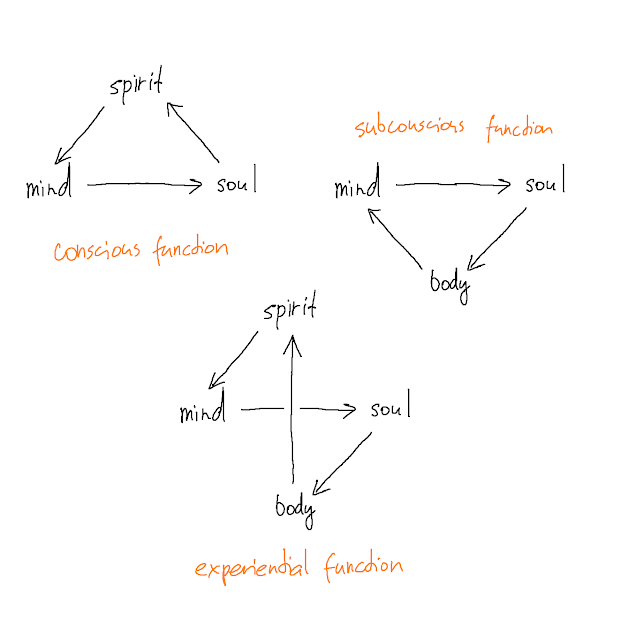
The four agents are organizes in the following directed graph:

We call it the Human Function Scheme (HFS for short). The arrows represent directions of information flow from one agent to another.

Postulate 1. Human function is marked by internal information processing within each of the four agents as well as exchange of information along the arrows of HFS. 

Postulate 2. When a human being is engaged in a particular activity, information flows between the agents in consistent cyclic patterns. Change of activity may change these patterns. 

Postulate 3. These cyclic patterns are made of three fundamental ones - the three cycles of HFS.

The cycles referred to in Postulate 3 are:

Whatever we claim to perceive consciously, is information processed in the Spirit. There are two arrows going into Spirit. Information flowing from Body to Spirit is the sensory ingredient of human's conscious perception. Information flowing from Soul to Spirit is the non-sensory ingredient human's conscious perception, such as thoughts, logical essence, etc. Rigorous research is needed to be able to develop a more refined distinction between these two ingredients of our conscious perception. We will hitherto distinguish them using the terms concrete perception (for Body to Spirit) and abstract perception (for Soul to Spirit). 

The arrow going out of Spirit is the channel through which our conscious impacts human function. We call information flowing along this arrow Will. The rest of the arrows have names too: subconscious perception (for Body to Mind), abstraction (for Mind to Soul), concretization (for Soul to Body).

There terms are somewhat suggestive of the role that the arrows of HFS play in human function. A better understanding of this role will be achieved when describing different types of human function in the context of HFS. 
 

Read More

Noetherian Forms

Link to a plenary talk on noetherian forms at a BRICS conference (2021): slides of the talk, recording of the talk.

Link to a talk on noetherian forms at the PALS seminar (2020): written summary, recording of the talk.

Noetherian forms are mathematical structures defined by self-dual axioms, that include all lattices, Janelidze-Marki-Tholen semi-abelian categories and Grandis exact categories. They can be seen as a realization of Saunders Mac Lane's hypothesis from his 1950 paper on Duality for Groups that self-dual axioms can be found to treat isomorphism theorems for non-abelian groups, as this is realized for abelian groups with the notion of an abelian category. Abelian categories are actually given by the overlap of semi-abelian and exact categories.

The term "noetherian" refers to the fact that these forms can seen as a fulfilment of Emmy Noether's program to "disregard the elements and operations in algebraic structures in favor of selected subsets, linked to homomorphisms between structures by the homomorphism and isomorphism theorems" - quote from Colin Maclarty's article.

See this list for relevant papers in this research area.

Work in progress and current conjectures / open questions regarding noetherian forms:

• Noetherian forms found for the category of sets - a paper on this is in preparation. Conjecture: these forms are present already for an arbitrary topos.
• The category of Hilbert spaces and continuous linear maps is an additive category, but not an abelian category. Conjecture: it nevertheless admits a noetherian form. Question: if there is indeed such noetherian form, is it of any use for quantum mechanics / quantum field theory?

Read More

Abstract Structures in Mathematics and Music

These are notes for my online discussion with Georgian Student Parliament on Tuesday 7 December, 2021, organized by Nina Tsatsanashvili. All photos in this post are from Wikipedia. 

If you look up the word "structure" on the Google Dictionary, you will find the following definition: the arrangement of and relations between the parts or elements of something complex. When the "parts or elements" are subject to specific interpretation, we have at hand an "abstract structure". For example, consider a painting, which can be seen as an arrangement of colors. For instance, Leonardo da Vinci's Mona Lisa:

This is not an abstract structure, since its constituents are specific colors that can be found on a specific poplar wood panel that currently resides in a gallery of the Louvre Museum in Paris. In contrast, Ludwig van Beethoven's Für Elise is an abstract structure, since the sounds that make up this musical piece are dependent on the interpretation of musical performer of the piece, as well as the instrument on which the piece is performed.

In this sense, abstract mathematics is similar to composition in music: in both cases one builds structures that are inherently abstract. The analogy goes further: a musical performer can be compared to an engineer, for instance, who produces concrete structures by means of concrete interpretations of the abstract mathematical structures.

 

In fact, the analogy goes even further than that. A completed piece of work in music, that is, a musical composition, is analogous to a "mathematical theory". A mathematical theory is an exploration of one or several special types of mathematical structures and their interrelation, similarly how in a musical composition one explores one or several types of musical structures and their interrelation. In both cases, abstract structures often organize into more abstract forms. 

As an example of a form of abstract structure in mathematics, consider the following diagram:

This diagram displays two mathematical structures, given by Fig. A and Fig. B. Each of them are abstract structures in the sense that the points and the arrows in each structure are subject to interpretation. The two structures have a similar form: they are both made out of points and arrows. Such structures in mathematics are called directed graphs. A mathematical theory that explores various different types of graphs and their interrelation is called graph theory. Graph theory, however, is not only about directed graphs. Other mathematical structures are also part of the theory, such as natural numbers, for instance. They arise by counting various different phenomena dealing with graphs: for example, by counting how many trajectories connect one point of the graph with another. 

Similarly, in a single musical composition, there is one (or several) main forms of musical structure, whose different manifestations are being explored, along with their interrelations, in the composition. What is the main form of musical structure in Für Elise?

     

Read More