2022 Academic Activities
Summary
- Initiated seven new collaborative research projects within the Mathematical Structures research programme, that includes researchers and postgraduate students from various universities in South Africa: operator semigroups, measure structures, metric frames, canonical extensions, ranked monoids, sum structures, lower topology.
- Supervised and co-supervised nine postgraduate students (two honors, two masters, and five phd).
- Represented South Africa at the General Assembly of the International Mathematical Union along with a colleague in Mathematics Education.
- In collaboration with colleagues and students, developed and delivered a successful math-music theatrical production for the celebration of the International Year of Basic Sciences for Sustainable Development. The production was supported by NITheCS, ASSAf and DSI.
- Developed and delivered four national postgraduate courses online: SOFiA on python, mathematical structures (in collaboration), introductory set theory (in collaboration), category theory.
- Executed presidential duties for SAMS: chairing of SAMS council meetings, of the AGM, opening and closure of the SAMS congress, etc. Prepared and delivered presidential address at the AGM (in consultation with the SAMS Council) to give a direction to SAMS activities in the coming years.
- Elected as NITheCS associate co-representative, and in this role, served on the NITheCS management committee monthly meetings.
- Ran the national research programme in mathematical structures under NITheCS along with three other principal investigators in the research programme.
- Two co-authored papers published, one in Journal of Symbolic Logic. Co-authored paper in Order accepted for publication.
- Served on the programme committee of the international conference "Topology, algebra and categories in logic" held in Coimbra, Portugal.
- Gave two interviews (radio and youtube).
- Taught and co-taught and/or convened six modules at Stellenbosch University, including two engineering mathematics modules, one honors module and two third-year modules.
- Progress made on existing and new research projects and delivered talks on those.
- Carried out duties in the role as mathematical sciences programme coordinator and member of a university research committee.
- Carried out refereeing and editorial duties (not listed below).
November-December 2022
- Research discussion (9 December) with Dr. Christian Budde: started research project on the category theory of operator semigroups.
- Chaired the Annual General Meeting of the South African Mathematical Society (8 December).
- Gave a SAMS Congress talk on the noetherian form of sets.
- Gave opening and closing speeches at the 65th Congress of the South African Mathematical Society (6-8 December), held at Stellenbosch University.
- Gave an opening speech at the special meeting of the Mathematics section of National Graduate Academy (5 December).
- Chaired the fourth Council Meeting of the South African Mathematical Society (2 December).
- Conducted weekly 6-hour tutorial sessions in November for students in Foundations of Abstract Mathematics I for additional assessment opportunity.
- The paper on ordinal number systems fully published in the Journal of Symbolic Logic.
- Submitted author comments on the journal proofs of the paper on stack combinatorics (joint work with Helmut Prodinger and Francois van Niekerk). The paper is being published by Springer Order.
- Hosted research visit (18-20 November) of Dr. Cerene Rathilal. Started joint work on measure structures.
- Submitted a report on the Mathematical Structures Research Programme at NITheCS and delivered a talk at the NITheCS Associates Workshop on the progress of the research programme.
- Made progress with Kishan Dayaram on diagram lemmas in the context of noetherian forms.
- Fundamano production (4 November) was a success -- full house attendance and well received. See: videos, press release.
September-October 2022
- Gave a talk on at the "Topology, Algebra, and Category Theory" international conference (19-22 September) dedicated to the 65th birthday of Themba Dube. The subject of the talk was metric frames.
- Supervised original honors projects of Gregor Feierabend and Gideo Joubert.
- Gave a semester honors course on Logic.
- Taught the English group of Engineering Mathematics 242 in the second semester of 2022.
- Chaired the third Council Meeting of the South African Mathematical Society (7 October).
- Hosted research visit (20 September - 8 October) of my PhD student, Noluntu Baart, to work on deductive reasoning in intermediate-phase mathematics education.
- Hosted research visit (9 October - 9 December) of my PhD student, Kishan Dayaram, to make progress on three joint papers.
- Hosted research visit (9-26 October) of Dr. Partha Pratim Ghosh. Joint work on canonical extensions started.
- Rehearsed and prepared for the Fundamano production in a team of students. This is a theatrical production bringing mathematics on stage, celebrating the international year for basic sciences.
- Drafted a paper based on the research on the category of near-vector spaces (co-authored with my MSc student, Daniella Moore, and the co-supervisor, Dr. Sophie Marques).
- Gave a National Graduate Academy course on category theory. Click here for videos and lecture notes.
- Gave a South African Theory School course on mathematical structures (jointly with Dr. Cerene Rathilal and Dr. Partha Pratim Ghosh). Click here for videos and lecture notes.
- Spoke on "Is Maths Trauma a real thing?" at the radio show Weekend Breakfast with Refiloe Mpakanyane. Click here for the podcast.
July-August 2022
- Organised a Research Workshop (5 July) on the occasion of visit (5 July) of Dr. Francois Schulz. Collaboration started on ranked monoids.
- Organised a Research Workshop (14 July) on the occasion of the research visit of Prof. Dharmanand Baboolal and Dr. Cerene Rathilal. Collaboration started on metric frames.
- Represented South Africa at the General Assembly of the International Mathematical Union (July 3-4, the report of the meeting is available here).
- Gave the August NITheCS mini-school on Elementary Introduction to Set Theory together with Dr. Amartya Goswami.
- Gave a Foundations of Abstract Mathematics I seminar on arithmetic and proof composition.
- Started research on the category of near-vector spaces (joint work with Dr. Sophie Marques and Daniella Moore).
- Leading programme renewal discussions in Mathematics in the second semester of 2022.
May-June 2022
- The paper on matrix taxonomy was published in Theory and Applications of Categories.
- Hosted research visit (1-4 June) of Dr. Charles Msipha to advance progress on sum structures.
- Continued research on a noetherian form of sets -- see the updated paper.
- Chaired the second Council Meeting of the South African Mathematical Society (26 May).
- Prepared an International Year for Basic Sciences for Sustainable Development project, which would later be called Fundamano. The project is listed on the official website of this international initiative. Dr. Charles Msipha and Dr. Sophie Marques are co-founders of the project.
- Elected as a NITheCS Associate Representative. Duties include serving on the NITheCS Management Committee (meetings are held monthly).
- Served on the programme committee of the international conference "Topology, algebra and categories in logic" held in Coimbra, Portugal.
March-April 2022
- Revisited research on a noetherian form of sets (joint work with Dr. Francois van Niekerk).
- Organised a Research Workshop on Monoidal Sum Structures at Stellenbosch University (20-25 March) and hosted the visit of Dr. Charles Msipha (Tshwane University of Technology). See the Mathematical Structures Research Programme website for further information. Two research projects dealing with sum structures were initiated at this workshop.
- Organised a Research Workshop on Lower Topology at Stellenbosch University (3-10 April) and hosted the visit of Dr. Amartya Goswami and Ms. Micheala Hoenselaar (University of Johannesburg). A research project on lower topology was initiated at this workshop.
- Gave an interview at the Meet a Mathematician series (see https://youtu.be/lOLIc8Jnja4).
- Supervised a 3rd year research project by Jean du Plessis (under Foundations of Abstract Mathematics II).
January-February 2022
- Serving on the Subcommittee B of the Research Committee of Stellenbosch University for 2022.
- Serving on the Programme Committee of the Faculty of Science of Stellenbosch University for 2022.
- Setting up Mathematical Structures Research Programme at the National Institute for Theoretical and Computational Sciences, along with Prof. Yorick Hardy, Dr. Partha Pratim Ghosh, and Dr. Cerene Rathilal.
- Delivered online lecture series Python-Based Introduction to Mathematical Proofs for the The 12th CHPC Introductory Programming School and The 4th NITheCS Summer School on the Foundations of Theoretical and Computational Science.
- Teaching Engineering Mathematics 214 (together with Dr. Liam Baker, Dr. Ronalda Benjamin, and Dr. Michael Hoefnagel) in the first semester and giving a Foundations of Abstract Mathematics I seminar in Mathematical Reasoning in the first term. Also teaching a third-year module, Topology, in the first semester.
- Convening Foundations of Abstract Mathematics I & II (year modules) and Topology (semester module) in 2022.
- Started/resumed (co-)supervision of the following postgraduate students: Noluntu Baart (PhD), Roy Ferguson (MSc), Kishan Dayaram (PhD), Paul Hugo (PhD), Brandon Laing (PhD), Daniella Moore (MSc), Ineke van der Berg (PhD).
- The paper on ordinal number systems appeared online in the Journal of Symbolic Logic (joint work with Ineke van der Berg).
- Assumed the role of the President of the South African Mathematical Society for the term 2022-2023. Chaired the first Council meeting (11 Feb).
- Under the research assistantship of Gregor Feierabend, the first prototype of a Haskell implementation of the SOFiA proof assistant was produced. See source code on GitHub or the live software.
Resilience (Opus 1015)
- Light sources (light bulbs, lanterns, etc.): ideas that could help you get through the difficult times
- Switched off TV screen with headphones over it: the feeling of emptiness
- Guns, glasses and the helmet: self-defense mechanisms
- Male and Female characters: your body (male character) and your soul (female character)
The Proof Course: Lecture 2
Many real-life situations lead us to considering a mathematical problem dealing with finding all possible numbers \(x\) satisfying a certain formula. In most primitive cases, this formula is an equation involving basic arithmetic operations (like the one we considered in Lecture 1). As an example of a formula that does not fall in this category, consider the following one:
\(x<y^2\) for every value of \(y\) (Formula A)
In other words, the formula expresses the property that no matter what value of \(y\) we pick, we will always have \(x<y^2\). Let us write this purely symbolically as follows (so that it looks more like a formula!):
\(y\Rightarrow x<y^2\) (symbolic form of Formula A)
In general, the symbol "\(\Rightarrow\)" describes logical implication of statements. Here the implication is: if \(y\) has a specific value then \(x<y^2\). In the symbolic form above, the assumption that \(y\) has a specific value is expressed by just writing \(y\) on the LHS (left-hand-side) of the implication symbol "\(\Rightarrow\)". Since we are not giving any further detail as to which specific value does \(y\) have, the implication must not be dependent on such detail, and hence the RHS (right-hand-side), \(x<y^2\), must hold for all values of \(y\). Note however that this type of symbolic forms, where variables are allowed to be written on their own like in the LHS of the implication symbol above, is not a standard practice. We will nevertheless stick to it, as it makes understanding proofs easier.
So, what is the solution of Formula A? If \(x<y^2\) needs to hold for every value of \(y\), then in particular, it must hold for \(y=0\), giving us \(x<0^2=0\). This can be written out purely symbolically, as a proof:
- \(y\Rightarrow x<y^2\)
- \(x<0^2\)
- \(x<0\)
- \(x<0\)
- \(y\Rightarrow 0\leqslant y^2\)
- \(y\Rightarrow x<y^2\)
- \(y\Rightarrow x<y^2\)
- \(x<0^2\)
- \(0^2=0\)
- \(x<0\)
The Proof Course: Lecture 1
In this blog-based lecture course we will learn how to build mathematical proofs.
Let us begin with something simple. You are most likely familiar with "solving an equation". You are given an "equation", say \[x+2=2x-3\] with an "unknown" number \(x\) and you need to find all possible values of \(x\), so that the equation holds true. You then follow a certain process of creating new equations from the given one until you reach the solution: \[2+3=2x-x\] \[5=x\] This computation is in fact an example of a proof. To be more precise, there are two proofs here: one for proving that
if \(x+2=2x-3\) then \(x=5\) (Proposition A),
and the other proving that
if \(x=5\) then \(x+2=2x-3\) (Proposition B).
The first proof is the same as the series of equations above. The second proof is still the same series, but in reverse direction. The two Propositions A and B together guarantee that not only \(x=5\) fulfills the original equation (Proposition B), but that there is no other value of \(x\) that would fulfill the same equation (Proposition A). It is because of the presence of these two proofs in our computation that we can be sure that \(x=5\) is indeed the solution of the equation \(x+2=2x-3\).
In general, a proof is a series of mathematical formulas, like the equations above. However, in addition to a "vertical" structure of a proof, where each line displays a formula that has been derived from one or more previous lines, there is also a "horizontal" structure, where each line of a proof has a certain horizontal offset. This is, at least, according to a certain proof calculus formulated by someone by the name of Fitch. There are other ways of defining/describing proofs; in fact, there is an entire subject of proof theory, which studies these other ways. We will care little about those other ways and stick to the one we started describing, as it is closest to how mathematicians actually compose proofs in their everyday job.
So where were we? We were talking about "vertical" and "horizontal" structure of a proof. Not to complicate things too much at once, let us first get a handle on the vertical structure of proofs, illustrating it on various example proofs that have most primitive possible horizontal structure. We will then, slowly, complexify the horizontal structure as well.
For Proposition A, the proof goes like this:
- \(x+2=2x-3\)
- \(2+3=2x-x\)
- \(5=x\)
The numbers at the start of each line are just for our reference purposes, they do not form part of the proof. Line 2 is a logical conclusion of Line 1: if \(x+2=2x-3\) then it must be so that \(2+3=2x-x\), since we could add \(3\) to both sides of the equality and subtract \(x\) as well – a process under which the equality will remain true if it were true at the start.
Line 3 is (again) a logical conclusion of Line 2: since \(5=2+3\) and \(2x-x=x\), so if the equality in Line 2 were true then the equality in Line 3 must be true as well.
A series of lines of mathematical formulas where every next line is a logical conclusion of the previous one or more lines, is a mathematical proof with simplest possible horizontal structure. We will call such proofs "basic".
Proposition B also has a basic proof:
- \(5=x\)
- \(2+3=2x-x\)
- \(x+2=2x-3\)
\(x=5\) and \(x+2=2x-3\),
\(x=5\) or \(x+2=2x-3\),
Pure Mathematics: Job Description
The SOFiA Proof Assistant Project
Background
The goal of this project is to build a proof assistant based on the SOFiA proof system, where the capital letters in SOFiA stands for Synaptic First Order Assembler (the purpose of the lower-case "i" will be explained further below). The use of terms "synapsis" and "assembler" is a suggestion of Brandon Laing, who wrote an MSc Thesis, "Sketching SOFiA" (2020), where the notion of an assembler was introduced: an assembler is the monoid of words in a given alphabet, seen as a monoidal category. The main result of his MSc Thesis was a characterization of assemblers using intrinsic properties of a monoidal category. An assembler gives a robust theoretical framework which guides the syntactical structure of the SOFiA proof system. The latter has been refined through a series of discussions with Louise Beyers and Gregor Feierabend in 2021, after which the first computer implementation of the SOFiA proof system was produced, based on the Python programming language. You can learn about it here. In January 2021, Gregor Feierabend developed a self-contained Haskell implementation, with user interface and documentation, which can be accessed here.
Overview of the SOFiA Proof System
- Making an assumption (no restrictions except that the assumption must be a valid SOFiA expression).
- Restating an already stated SOFiA expression.
- Recalling a theorem or an axiom, external to the proof.
- Equating a stated SOFiA expression with itself.
- Synapsis: stepping out of an assumption block (this allows to conclude quantified statements, as well as implications).
- Application a SOFiA expression (this allows to conclude from quantified statements as a generalization of the modus ponens rule).
- Substitution: substituting SOFiA expressions within each other based on already stated equalities.
These deduction rules do not include rules for disjunction or fallacy. The latter can be implemented as axiom schemes. So at its base, the SOFiA proof system embodies a bit less than intuitionistic logic. This is marked by the appearance of lower-case "i" in "SOFiA". Note however that because in the SOFiA syntax there is no distinction between "objects" and "statements about objects", the SOFiA proof system is not quite the same as the usual proof system of a first-order logic, although in a loose sense SOFiA does have the structure of a first-order language. One of the key differences with standard first-order languages is that in SOFiA one does not introduce additional relational or functional symbols. Instead, one may write any sequence of allowed characters in SOFiA which can be given the intended meaning of a relational or a functional symbol by means of axioms. Possibility for a sound and complete embedding of any first-order logic in SOFiA still needs to be proved and is currently one of the founding themes of PhD research by Brandon Laing.
Developing the Proof Assistant
The current version(s) of the SOFiA proof assistant have the following shortcomings, which are to be addressed in the near future:
- The proofs can only be built line-by-line, it is currently not possible for the computer to fill the missing lines. This applies to both the Python and Haskell implementations.
- The Python implementation source code is messy and there is currently no documentation.
- The Haskell implementation contains bugs.
- There Python implementation does not have a user interface.
- Python and Haskell implementations come with modules for Boolean Logic and Peano Arithmetic, but they do not yet come with a module for Set Theory.
Bracket Notation for Mathematical Proofs
The bracket notion for mathematical proofs is an adaptation of the Fitch notation for Gentzen's natural deduction proof system. It has led to the development of the SOFiA proof assistant. This post brings together some videos explaining the bracket notation and the first-order formal language for mathematics in the context of the bracket notation.
1. General Overview
2. Building Blocks for Statements
3. Examples of Forming Statements
4. Examples of Forming Statements (Continued)
5. Concluding Quantified Statements
6. Concluding from Quantified Statements
Category Theory Course 2022
Here you will find the content for the Category Theory course given under the National Graduate Academy NGA-Coursework of the CoE-MaSS. The lectures are on Saturdays 9:00-11:00.
Register here to receive the Zoom link for joining the lectures
There is also a Discord channel for this course, which you can find on the Discord server of the NGA-Coursework project.
This is a video-based course aimed at post-graduate students and as well academics interested to learn about category theory, with live participation of the audience shaping the content of the course. For a reading course at the South African honors level, see:
- Category Theory: A First Course by George Janelidze
- Elementary Introduction to Category Theory by Amartya Goswami and Zurab Janelidze
Lecture 1: Categories
Lecture 2: Functors
Lecture 3: Natural Transformations
Lecture 4: Adjunctions
Lecture 5: Limits
Lecture 6: Duality
Lecture 7: Yoneda Embedding
Lecture 8: Equivalence of Categories
Mathematical Structures Course 2022
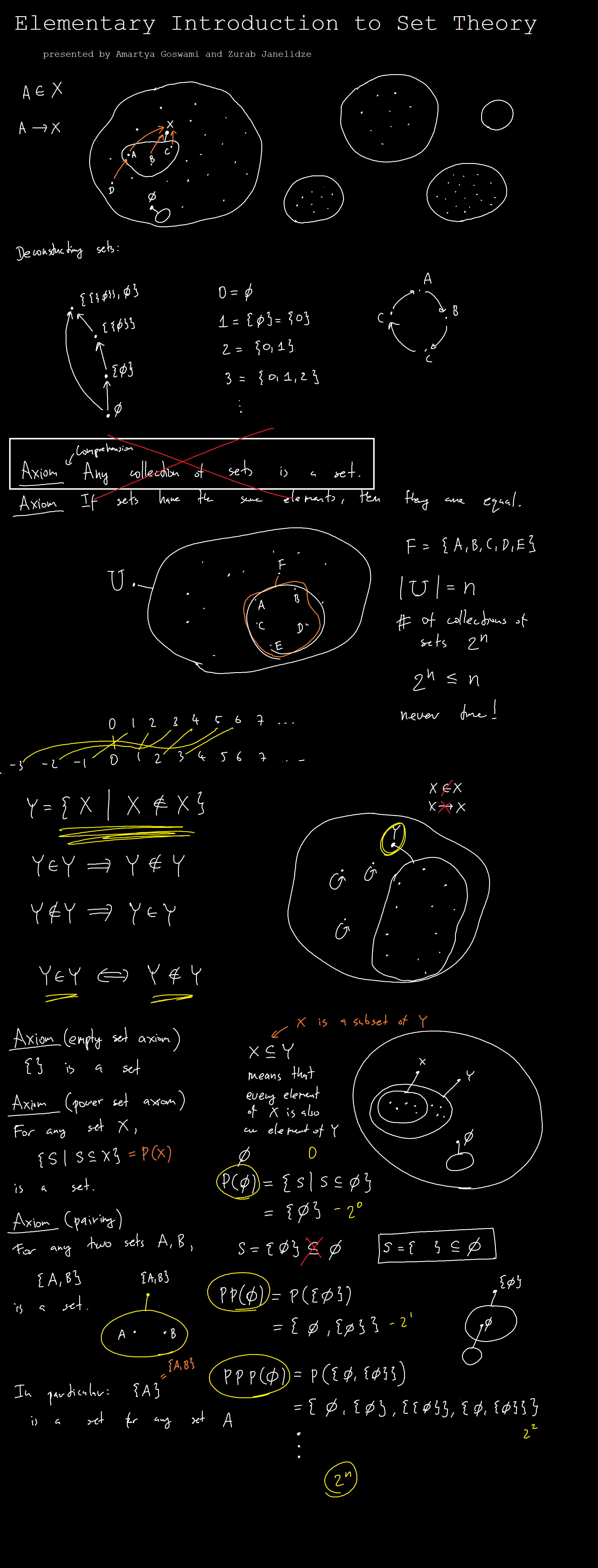
Elementary Introduction to Set Theory
This is the blog post of the 2022 August NITheCS Mini-School. Let us begin with some useful links:
- Lecture notes on universes of sets (introductory)
- Some videos explaining the concepts from the lecture notes above
Lecture 1
Lecture 2
Lecture 3
Lecture 4
Guitarist, Contemplation and Camille
Guitarist
This picture symbolizes a human state when one is working on a routine task, while one's mind looks into the bigger picture of things. While guitarists hands are busy playing on the guitar, his eyes are looking into the open space from a balcony. The fence of the balcony symbolizes the restrictions imposed on us by the necessity of a routine task.
Contemplation
This picture shows the back of a woman with yellow hair, in a stylish red dress, gazing at the white moon. The hair is blowing in a light wind. Mountains covered in snow are in the background. Her outfit is certainly not a match for the cold weather, but contemplation will keep her body warm. This picture symbolizes that deeper things in life can give us physical strength.
Camille
Waves
This freehand digital artwork represents the idea that significant change requires restructuring of foundations. The solid ground on the right middle side of the picture (the foundations) dissolves into an uproar of waves that illustrate the process of restructuring, which may appear to be chaotic. Going back from the left to the right side of the picture the waves subside into (new) foundations.
Beautiful Roses (opus 1601)
- The bud with the sun in the background shown at the start of the video represents an idea that starts the creative process.
- The rose opening up, which is repeated three times in the video, represents the anticipation of the fulfillment, the fulfillment, and the reflection on the fulfillment of the creative process.
- The first character, dressed in conservative clothes, symbolizes the mind. The second character symbolizes the soul. The first character is reserved in her display of emotions as well as in her interaction with the roses. The second character is spontaneous and emotional, who interacts more intimately with the roses and displays enjoyment in such interaction. These represent the rational approach of the mind and the contrasting intuitive approach of the soul in a creative process.
- The first character wears black top throughout the video. The second character wears brighter tops. The first represents the critical approach of the mind and the struggles of the creative process, while the second represents the positive approach of the soul and the joy of the creative process. The positive/critical disposition of the soul versus the mind is symbolized also in the brighter lighting background for the second character versus the first character.
- For the most part of the video the character representing the mind has roses separated in bottles in the foreground. This represents the attitude of the mind to concentrate on the details in isolation from each other. The character representing the soul is, in contrast, shown with a bucket of flowers. This symbolizes the holistic approach of the soul in the creative process. The single flower that the second character appears to have isolated from the bucket symbolizes the driving idea behind the creative process.
- At the end of the video, the flowers in front of the character representing the mind are no longer separated in their bottles. Instead they appear lying in a heap in front of her, with one flower from the heap in her hands. This represents the conclusion of the creative process, when the mind dismisses the details and brings them all together, leading to the emergence of the contour of the bigger picture as a detail of its own.
- Just before the last scene, the character representing the soul passes the single rose she is holding towards the screen. This symbolizes disengagement of the soul at the end of the creative process. In the final scene, however, the other character remains with the roses. For the first time here, she smiles, but momentarily, while smelling the flower she is holding. This symbolizes that what remains after conclusion of the creative process is just mental image of what has been created. The excitement has subsided and there is only one emotion left, the unique positive experience of the mind in the process, which lasts only for one moment, making that moment worth the creative process: the feeling of accomplishment.
Reverse Prime Composite Numbers
The Transition from High School Mathematics to University Mathematics
These are notes in progress for a talk given at the online user group conference of the advanced programme mathematics organized by ieb (19 February 2022)
1. Introduction
2. Misleading Questions
3. Factual Teaching vs Insightful Teaching
- "sketch" instead of "graph" (or "sketch of the graph").
- Wilson says "-3 is not included" (it is rather the paint (-3,-1) that is not included in the graph) but "4 is included" (similarly, 4 is merely the x-coordinate of the point included in the graph).
- Wilson says that the domain is "where your graph is on the x-axis", and "range is where the graph is on the y-axis".
- Wilson says "if it is not defined, we put a round bracket, if it is defined, we put a square bracket".
6. Final Note ♪
7. Some Feedback from Students
Python-Based Introduction to Mathematical Proofs
1. What is a Mathematical Proof?
- discover new mathematical knowledge,
- analyze existing mathematical knowledge,
- verify truthfulness of a piece of mathematical knowledge.