This piece is to remind you of resilience, or toughness. Life is not a straight path and there come moments when the best you can do is endure. This requires bring out the fighter within you. It may also require you to stay focused.
Look out for the following objects in the video, which carry the symbolism as described below:
Light sources (light bulbs, lanterns, etc.): ideas that could help you get through the difficult times
Switched off TV screen with headphones over it: the feeling of emptiness
Guns, glasses and the helmet: self-defense mechanisms
Male and Female characters: your body (male character) and your soul (female character)
Many real-life situations lead us to considering a mathematical problem dealing with finding all possible numbers \(x\) satisfying a certain formula. In most primitive cases, this formula is an equation involving basic arithmetic operations (like the one we considered in Lecture 1). As an example of a formula that does not fall in this category, consider the following one:
\(x<y^2\) for every value of \(y\) (Formula A)
In other words, the formula expresses the property that no matter what value of \(y\) we pick, we will always have \(x<y^2\). Let us write this purely symbolically as follows (so that it looks more like a formula!):
\(y\Rightarrow x<y^2\) (symbolic form of Formula A)
In general, the symbol "\(\Rightarrow\)" describes logical implication of statements. Here the implication is: if \(y\) has a specific value then \(x<y^2\). In the symbolic form above, the assumption that \(y\) has a specific value is expressed by just writing \(y\) on the LHS (left-hand-side) of the implication symbol "\(\Rightarrow\)". Since we are not giving any further detail as to which specific value does \(y\) have, the implication must not be dependent on such detail, and hence the RHS (right-hand-side), \(x<y^2\), must hold for all values of \(y\). Note however that this type of symbolic forms, where variables are allowed to be written on their own like in the LHS of the implication symbol above, is not a standard practice. We will nevertheless stick to it, as it makes understanding proofs easier.
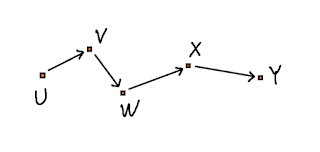
So, what is the solution of Formula A? If \(x<y^2\) needs to hold for every value of \(y\), then in particular, it must hold for \(y=0\), giving us \(x<0^2=0\). This can be written out purely symbolically, as a proof:
\(y\Rightarrow x<y^2\)
\(x<0^2\)
\(x<0\)
However, as we know from Lecture 1 already, this proof only proves that if Formula A is true then \(x<0\). In order for \(x<0\) to be the solution of Formula A, we also need to prove that if \(x<0\) then Formula A is true. Well, since \(0\leqslant y^2\) is true for every \(y\), combining \(x<0\) with \(0\leqslant y^2\) we will get \(x<y^2\), as required in Formula A. So the proof is:
\(x<0\)
\(y\Rightarrow 0\leqslant y^2\)
\(y\Rightarrow x<y^2\)
Note that it seems as if this proof violates our requirement that in a basic proof, every line except the first one must be a logical conclusion of the previous one or several lines. Line 2 does not necessarily seem to be a conclusion of Line 1. Instead, it is simply a general true fact that does not seem to logically depend on Line 1 at all: it says that the square of every number is greater or equal to \(0\). We can account for such situations by agreeing that "several" in "one or several lines" includes the case of "\(0\) many". So in a basic proof we can also include lines that recall facts we know. If we had not done that in the above proof, we would have to skip from Line 1 directly to Line 3, and it may not have been so clear how does one logically conclude Line 3 from Line 1. So we allow inclusion of known facts as lines in a basic proof for the sake of clarity. Knowing this, we might want to make the first proof clearer by inserting one such line:
In this blog-based lecture course we will learn how to build mathematical proofs.
Let us begin with something simple. You are most likely familiar with "solving an equation". You are given an "equation", say \[x+2=2x-3\] with an "unknown" number \(x\) and you need to find all possible values of \(x\), so that the equation holds true. You then follow a certain process of creating new equations from the given one until you reach the solution: \[2+3=2x-x\] \[5=x\] This computation is in fact an example of a proof. To be more precise, there are two proofs here: one for proving that
if \(x+2=2x-3\) then \(x=5\) (Proposition A),
and the other proving that
if \(x=5\) then \(x+2=2x-3\) (Proposition B).
The first proof is the same as the series of equations above. The second proof is still the same series, but in reverse direction. The two Propositions A and B together guarantee that not only \(x=5\) fulfills the original equation (Proposition B), but that there is no other value of \(x\) that would fulfill the same equation (Proposition A). It is because of the presence of these two proofs in our computation that we can be sure that \(x=5\) is indeed the solution of the equation \(x+2=2x-3\).
In general, a proof is a series of mathematical formulas, like the equations above. However, in addition to a "vertical" structure of a proof, where each line displays a formula that has been derived from one or more previous lines, there is also a "horizontal" structure, where each line of a proof has a certain horizontal offset. This is, at least, according to a certain proof calculus formulated by someone by the name of Fitch. There are other ways of defining/describing proofs; in fact, there is an entire subject of proof theory, which studies these other ways. We will care little about those other ways and stick to the one we started describing, as it is closest to how mathematicians actually compose proofs in their everyday job.
So where were we? We were talking about "vertical" and "horizontal" structure of a proof. Not to complicate things too much at once, let us first get a handle on the vertical structure of proofs, illustrating it on various example proofs that have most primitive possible horizontal structure. We will then, slowly, complexify the horizontal structure as well.
For Proposition A, the proof goes like this:
\(x+2=2x-3\)
\(2+3=2x-x\)
\(5=x\)
The numbers at the start of each line are just for our reference purposes, they do not form part of the proof. Line 2 is a logical conclusion of Line 1: if \(x+2=2x-3\) then it must be so that \(2+3=2x-x\), since we could add \(3\) to both sides of the equality and subtract \(x\) as well – a process under which the equality will remain true if it were true at the start.
Line 3 is (again) a logical conclusion of Line 2: since \(5=2+3\) and \(2x-x=x\), so if the equality in Line 2 were true then the equality in Line 3 must be true as well.
A series of lines of mathematical formulas where every next line is a logical conclusion of the previous one or more lines, is a mathematical proof with simplest possible horizontal structure. We will call such proofs "basic".
Proposition B also has a basic proof:
\(5=x\)
\(2+3=2x-x\)
\(x+2=2x-3\)
Just as before, every next line is a logical conclusion of the previous one.
What about the first line (in each proof)? If the first line were to also satisfy the requirement that it is a logical conclusion of the previous lines, then, since there are no lines before the first line, it would appear that the first line is true on its own, without a need for justification. If course, in both proofs this is false: in the first proof, we cannot claim that Line 1 is true. Truth of Line 1 in the first proof depends on the value of \(x\). Without knowing anything about the value of \(x\), we cannot claim that \(x+2=2x-3\), since if, say, \(x=0\), then \(x+2=2x-3\) is clearly false. The same for the second proof - we cannot claim that Line 1 is true. Instead, the role of the first line in each of the proofs is to "assume" they are true, and then see what conclusions can be drawn from such assumption. Recall that Proposition B, for instance, states that if \(x=5\) then \(x+2=2x-3\). It does not state that
\(x=5\) and \(x+2=2x-3\),
or that
\(x=5\) or \(x+2=2x-3\),
and so on. So in a basic proof the first line will always be an assumption, unlike the rest of the lines, which are conclusions from the previous one or several lines.
What does a "pure mathematician" do? A shoemaker makes shoes, a musician makes music, an applied mathematician uses mathematics to solve some real-life problems... Each of these job descriptions have some sort of measurable output. What is such output for a pure mathematician?
Some will say that a pure mathematician solves problems in mathematics, i.e., mathematical problems that are not necessarily related to "real life". This does not do justice to the efforts of a pure mathematician: if you are keen to solve problems, rather solve real-life problems! The problem is that the language in which these "pure" mathematical problems are solved is such that it cannot (always) be used to solve the "real-life" problems. A pure mathematician wants to solve only those problems whose solutions are expressed in a pure mathematical language. This does not do justice to the efforts of a pure mathematician either: what a picky attitude! Besides, solve-a-problem style job description applies to every other job. Indeed, any job for which you expect to get paid requires some sort of problem-solving.
The job description of a pure mathematician is actually quite straightforward. A pure mathematician builds "proofs". A proof is a discussion that reaches a certain conclusion with a life-time guarantee of truthfulness of this conclusion. In no other discipline are you able to establish proofs with such a guarantee. Surely having a certainty in a certain fact is a useful thing in any area of life. Unfortunately though, as soon as your conclusions come close to describing how something in "real life" works, their certainty can no longer be guaranteed, i.e., they step out of the reach of pure mathematics. Still, pure mathematics is extremely useful in establishing the real-life-like close-to-certain conclusions, otherwise the disciplines such as applied mathematics, physics, chemistry, and many others, would hardly make any progress (for those who may not be aware of this, these disciplines, as well as many others, rely a lot on conclusions proved in pure mathematics).
The conclusions that a proof proves are called "theorems". Then there are "definitions", which are essentially shortcuts for building complex proofs. Now a proof starts with certain assumptions (always, in fact, for those who may have been deceived that unlike religion, science does not rely on unproved assumptions, but this is a topic for an entirely different discussion...). The universal assumptions, i.e., those that are used over and over in many different proofs, are called "axioms". Part of the task of a pure mathematician is coming up with appropriate definitions and axioms. In the end, they are to be used in a proof, otherwise, they are useless. Solving a pure mathematical problem is all about finding a proof: of a theorem, its negation, or if the theorem has not been precisely stated, finding a precise statement and then its proof. So fair and square, a pure mathematician is someone who builds proofs!
The goal of this project is to build a proof assistant based on the SOFiA proof system, where the capital letters in SOFiA stands for Synaptic First Order Assembler (the purpose of the lower-case "i" will be explained further below). The use of terms "synapsis" and "assembler" is a suggestion of Brandon Laing, who wrote an MSc Thesis, "Sketching SOFiA" (2020), where the notion of an assembler was introduced: an assembler is the monoid of words in a given alphabet, seen as a monoidal category. The main result of his MSc Thesis was a characterization of assemblers using intrinsic properties of a monoidal category. An assembler gives a robust theoretical framework which guides the syntactical structure of the SOFiA proof system. The latter has been refined through a series of discussions with Louise Beyers and Gregor Feierabend in 2021, after which the first computer implementation of the SOFiA proof system was produced, based on the Python programming language. You can learn about it here. In January 2021, Gregor Feierabend developed a self-contained Haskell implementation, with user interface and documentation, which can be accessed here.
Overview of the SOFiA Proof System
The SOFiA proof system is an adaptation of the Fitch notation for natural deduction. The main novelty of the SOFiA proof system is the use of variables as statements, which leads to reducing quantified statements to implications. This allows unification of deduction rules for implication with those for the universal and existential quantifiers. The basic deduction rules for the proof system then are:
Making an assumption (no restrictions except that the assumption must be a valid SOFiA expression).
Restating an already stated SOFiA expression.
Recalling a theorem or an axiom, external to the proof.
Equating a stated SOFiA expression with itself.
Synapsis: stepping out of an assumption block (this allows to conclude quantified statements, as well as implications).
Application a SOFiA expression (this allows to conclude from quantified statements as a generalization of the modus ponens rule).
Substitution: substituting SOFiA expressions within each other based on already stated equalities.
These deduction rules do not include rules for disjunction or fallacy. The latter can be implemented as axiom schemes. So at its base, the SOFiA proof system embodies a bit less than intuitionistic logic. This is marked by the appearance of lower-case "i" in "SOFiA". Note however that because in the SOFiA syntax there is no distinction between "objects" and "statements about objects", the SOFiA proof system is not quite the same as the usual proof system of a first-order logic, although in a loose sense SOFiA does have the structure of a first-order language. One of the key differences with standard first-order languages is that in SOFiA one does not introduce additional relational or functional symbols. Instead, one may write any sequence of allowed characters in SOFiA which can be given the intended meaning of a relational or a functional symbol by means of axioms. Possibility for a sound and complete embedding of any first-order logic in SOFiA still needs to be proved and is currently one of the founding themes of PhD research by Brandon Laing.
Developing the Proof Assistant
The current version(s) of the SOFiA proof assistant have the following shortcomings, which are to be addressed in the near future:
The proofs can only be built line-by-line, it is currently not possible for the computer to fill the missing lines. This applies to both the Python and Haskell implementations.
The Python implementation source code is messy and there is currently no documentation.
The Haskell implementation contains bugs.
There Python implementation does not have a user interface.
Python and Haskell implementations come with modules for Boolean Logic and Peano Arithmetic, but they do not yet come with a module for Set Theory.
The bracket notion for mathematical proofs is an adaptation of the Fitch notation for Gentzen's natural deduction proof system. It has led to the development of the SOFiA proof assistant. This post brings together some videos explaining the bracket notation and the first-order formal language for mathematics in the context of the bracket notation.
There is also a Discord channel for this course, which you can find on the Discord server of the NGA-Coursework project.
This is a video-based course aimed at post-graduate students and as well academics interested to learn about category theory, with live participation of the audience shaping the content of the course. For a reading course at the South African honors level, see:
This page contains resources for a SATACS course at NITheCS that runs over the second semester of 2022. The lectures take place on Zoom on Fridays 17:00-19:00. If you would like to join them, register here.
This picture symbolizes a human state when one is working on a routine task, while one's mind looks into the bigger picture of things. While guitarists hands are busy playing on the guitar, his eyes are looking into the open space from a balcony. The fence of the balcony symbolizes the restrictions imposed on us by the necessity of a routine task.
Contemplation
This picture shows the back of a woman with yellow hair, in a stylish red dress, gazing at the white moon. The hair is blowing in a light wind. Mountains covered in snow are in the background. Her outfit is certainly not a match for the cold weather, but contemplation will keep her body warm. This picture symbolizes that deeper things in life can give us physical strength.
Camille
This drawing shows two sides of Camille Vasquez, one of the lawyers defending Johnny Depp in the livestreamed trial of defamation of Johnny Depp in 2022. The picture shows a head and a body side-by-side. The head, with a thoughtful expression of the face, represents the successful lawyer. The body, in a formal dress, represents the celebrity status that she obtained during the trial. The white color of the outfit is a reminder of the white suit that she wore during her closing argument. The body and the head are flipped relative to each other to emphasize the contrast between what they represent. This artwork is a symbolism for the duality of being good at what you do and being famous.
This freehand digital artwork represents the idea that significant change requires restructuring of foundations. The solid ground on the right middle side of the picture (the foundations) dissolves into an uproar of waves that illustrate the process of restructuring, which may appear to be chaotic. Going back from the left to the right side of the picture the waves subside into (new) foundations.
The inspiration for this composition was a discussion with the Composer Hans Roosenschoon, during which I presented to him some of my musical works, and also had a chance to listen to some of his unpublished works. I composed the piece the next day after the discussion. It was originally intended to be only the first sketch of the composition.
This piece signifies beauty of creativity. The video shows two contrasting characters, which represent the mind and the soul in a creative process. The roses are the creation. They appear in different color, form and contexts, to signify diversity of creation. Thus, the video provides a symbolic interpretation of the process and product of creativity.
Elaboration of some of the symbolism in the video:
The bud with the sun in the background shown at the start of the video represents an idea that starts the creative process.
The rose opening up, which is repeated three times in the video, represents the anticipation of the fulfillment, the fulfillment, and the reflection on the fulfillment of the creative process.
The first character, dressed in conservative clothes, symbolizes the mind. The second character symbolizes the soul. The first character is reserved in her display of emotions as well as in her interaction with the roses. The second character is spontaneous and emotional, who interacts more intimately with the roses and displays enjoyment in such interaction. These represent the rational approach of the mind and the contrasting intuitive approach of the soul in a creative process.
The first character wears black top throughout the video. The second character wears brighter tops. The first represents the critical approach of the mind and the struggles of the creative process, while the second represents the positive approach of the soul and the joy of the creative process. The positive/critical disposition of the soul versus the mind is symbolized also in the brighter lighting background for the second character versus the first character.
For the most part of the video the character representing the mind has roses separated in bottles in the foreground. This represents the attitude of the mind to concentrate on the details in isolation from each other. The character representing the soul is, in contrast, shown with a bucket of flowers. This symbolizes the holistic approach of the soul in the creative process. The single flower that the second character appears to have isolated from the bucket symbolizes the driving idea behind the creative process.
At the end of the video, the flowers in front of the character representing the mind are no longer separated in their bottles. Instead they appear lying in a heap in front of her, with one flower from the heap in her hands. This represents the conclusion of the creative process, when the mind dismisses the details and brings them all together, leading to the emergence of the contour of the bigger picture as a detail of its own.
Just before the last scene, the character representing the soul passes the single rose she is holding towards the screen. This symbolizes disengagement of the soul at the end of the creative process. In the final scene, however, the other character remains with the roses. For the first time here, she smiles, but momentarily, while smelling the flower she is holding. This symbolizes that what remains after conclusion of the creative process is just mental image of what has been created. The excitement has subsided and there is only one emotion left, the unique positive experience of the mind in the process, which lasts only for one moment, making that moment worth the creative process: the feeling of accomplishment.
The story begins with an observation made to me by my father, on 22 February 2022, that it is a special date. Afterwards, I found out he was representing this date as 20220222 (year first, month and then day). In my original interpretation, it was 22022022. I was not satisfied just with the fact that this is a palindrome (a number which, when reversed, gives back the same number). So I looked into its prime factors: 22022022 = 2 x 3 x 11 x 2 x 3 x 11 x 333667. After a while of staring at this, I checked what would happen if I reversed 333667. That number (766333) turned out to be a prime as well! I learned afterwards that prime numbers whose reverse (in decimal notation) are prime, are called reverse primes. So then 22022022 is a composite reverse prime, i.e., a natural number who all prime factors are reverse primes. The question was: how special does this make the number 22022022? To be continued.
These are notes in progress for a talk given at the online user group conference of the advanced programme mathematics organized by ieb (19 February 2022)
1. Introduction
In my experience, what makes transition from school mathematics to university mathematics hard is the depth of engagement with mathematics that university mathematics requires of students, compared to the depth of engagement that school mathematics requires. Do you agree or disagree with the following thesis:
A school learner must understand school mathematics at the same depth that a university student is expected to understands university mathematics.
If you do not agree and think that a university student should understand university mathematics more deeply than a school learner understands school mathematics, this means that you expect a learner transitioning to university not only having to learn more advanced mathematics, but to understand it more deeply than they understand its foundation, the school mathematics. Is that possible?!
2. Misleading Questions
What hinders a school learner to understand school mathematics deeply? Learning is driven by assessment: eventually, the task of a school teachers is to bring a pupil to the point of passing the final exam paper. Learning happens through textbooks which engages learners in a learning process that is based on answering questions that resemble those in the final exam. So then, it is natural to conclude that the mathematical questions students have to work on, whether from the textbook or the exam, paint the image of the mathematics they are learning. What if these questions mislead the learner and provide them with a wrong image of mathematics?
Here we give some examples of questions that have a great potential of misleading the learners.
What is the next number in the sequence 0,1,2,3,4,5,6,7,...?
The school expects the answer to be 8. In actual mathematical reality, it can be any other number as well, since we have not given any restriction on the sequence apart from its first eight digits. There are 1669 entries on these eight terms in the Encyclopedia of Integer Sequences.
This question misleads a pupil to thinking that the first idea that comes to mind (which would be indeed 8 for most humans) is the right answer to a mathematical question, and hence, if no idea comes at first, then there is no way to answer a question.
What is the domain of the function f(x)=x^2?
The school expects the answer to be entire real line. In actual mathematical reality, a formula does not define a function uniquely. To have a function, you need to first name a domain (and a "codomain", which is not necessarily the same as the "range") and then, state the formula which is to be interpreted for the named domain and codomain. Otherwise, why the entire real line -- the domain could have been the complex plane just as well!
This question misleads a pupil to thinking that mathematical equations contain complete information about mathematical objects. This eventually results in them dismissing words in a complex logical statement, focusing on a flattened picture comprising of just the equations in the statement. For example, they read "if 1=2 then 3=4" as "1=2 and 3=4". The latter is a false statement. The former is not: from 1=2 we can indeed derive 3=4 (simply add 2 to both sides).
Solve the equation (x+3)/2=5.
The school expects the students to perform a sequence of manipulations eventually leading to the "answer" x=7. In actual mathematical reality, each step needs to be confirmed to be reversible to be certain that 7 is indeed a solution of the equation (that is it the only solution, is confirmed by the derivation).
This question misleads a pupil to thinking that solving an equation means applying some procedures in one direction. With this, not only the pupils do not understand the concept of a "solution", but they tend to think that any mathematical problem can be solved by a sequence of manipulations which need not be logically justified. This also results in them not understanding the difference between "implies" and "is equivalent to".
These are just some examples of misleading questions. There are many more!
3. Factual Teaching vs Insightful Teaching
Note:
"sketch" instead of "graph" (or "sketch of the graph").
Wilson says "-3 is not included" (it is rather the paint (-3,-1) that is not included in the graph) but "4 is included" (similarly, 4 is merely the x-coordinate of the point included in the graph).
Wilson says that the domain is "where your graph is on the x-axis", and "range is where the graph is on the y-axis".
Wilson says "if it is not defined, we put a round bracket, if it is defined, we put a square bracket".
In each of these examples we see a simplification of the language for pointing out something to the pupil. These simplifications may cost knowledge: a pupil who is not well familiar with the material receives logically incomplete information and hence enters into a mode of memorization where certain phrases are paired up with certain settings in a mathematical question. Instead of learning to actually comprehend the question, the learners become accustomed to break up the question in several keywords which in their memory relate (without any insight as to why) to some procedures that the learning needs to perform.
With this method of learning, which is present at university too, the learner/student comprehends mathematics as a set of memorized principles whose only application that they can experience is writing an exam. Mathematics for them is not something in which they can look for a story, an insight, or meaning.
Factual teaching vs insightful teaching compares well with learning music based on reading music notation vs based on listening to the instrument:
4. Contribution from Dr. Cerene Rathilal
5. Challenge, Passion and Hard Work
It is customary to think that pupils lose passion for mathematics when they encounter challenges in it. I do not believe this to be the case. To the contrary, I believe that people get inspired by challenge, as long as it stimulates intellect. Nobody has passion for something that is easy to get! My thesis is:
What kills mathematical passion in learners is realization that to overcome a mathematical challenge all it takes is routine hard word (e.g., memorization), instead of intellectual enquiry.
Sure, it is important for a learner to develop the skill of working hard. However, mathematics is not the right subject for that. Mathematics is supposed to be the subject that awakens a genius in a human being. There is even scientific evidence to back something that true mathematicians know very well: to be smart, you need to be lazy. The reason for this seemingly paradoxical relation is that if you are not lazy, you are likely to involve yourself with various activities that makes use of the rest of your body more than your brain. As a mathematician, the more mathematical research I do, the less I want to do anything else, including going to a shop to buy bread -- I become too lazy to even do that, not to mention doing admin at the university! On the other hand, when I force myself to do hard work with the admin (or physical exercise, which for the sake of winning time involves bicycling to the bread shop), I am no longer able to do mathematics effectively. My brain sort of flattens out -- I am not able to think sufficiently deeply any more.
Doing mathematics properly and working hard are in direct contradiction. Part of mathematical ingenuity is about finding a solution to a problem that saves your time. Laziness actually drives mathematical enquiry. But as soon as you do mathematics the right way, your brain releases chemicals which enable you to work for long hours, without having a feeling that you worked hard. You get exhausted, and yet you feel you did not work hard enough. That is the truth about mathematics.
When mathematics is taught through hard work, it kills passion simply because hard work kills mathematical creativity in a professional mathematics researcher too. If you are doing mathematics and you feel you are working hard, as far as I can tell, you are not doing actual mathematics.
A mathematical challenge is supposed to ignite passion and not kill it. If it kills passion, it may not be a challenge worth pursuing. In fact, research mathematicians use this principle to navigate their way in research: selection of which problem to pursue and which not to pursue is very much determined whether the problem ignites or kills passion.
Thus, when mathematics is done the right way, the diagram is:
challenge => passion ignites => hard work
When it is done the wrong way, the diagram becomes:
hard work => passion dies => challenge
6. Final Note ♪
In general, school mathematics is much about learning procedures to solve computational problems, without understanding why do those procedures work, not to mention a chance to self-discover the procedures. Intellectual effort of the student is reduced to writing in one's memory bank these procedures and practicing their application as far as answering exam questions is concerned.
Instead, university mathematics is more about understanding concepts intuitively, allowing a student to apply the understanding to solve a problem by self-discovering a procedure. Not only students are expected to explain why a procedure works, but they are also expected to come up with a procedure (a proof) which would confirm validity of a mathematical statement.
Those who have a talent for memorizing procedures usually lack the talent of creativity in mathematics, and vice versa. In other words, school mathematics favors learners with a certain intellectual profile, which is likely to exclude those who are capable of taking their mathematics studies at an advanced university level.
The issues discussed here do not only apply to transition from school mathematics to university mathematics. Similar issues arise in transition from undergraduate mathematics to postgraduate mathematics, and from postgraduate mathematics to research mathematics. In all cases, incorrect approach to mathematics leads to lack of sufficient foundation to advance to the next step.
7. Some Feedback from Students
The content of the first-year math courses is a lot of new work which builds onto the foundation that high school laid, therefore it was ideal to enter the first year with my mind still fresh from the matric exam the previous year. I personally found the way of learning maths in high school - listening in class, practising and using textbooks - quite similar to learning 1st-year math, only the workload increased and the pace at which it was presented. One big difference from high school is that you are given the free will to attend lectures and use your time wisely for practising problems. You are given examples to work through weekly, but it is basically up to the student if they want to make it their "homework" and that is what will separate the cream of the crop when they get tested. Thus if one did not practice self-discipline in high school, University is where they learn to. Another difference from high school is different lecturers for different courses with their own unique teaching styles. Compared to one high-school teacher, students now face the reality that they must adapt to new lecturers for every course each promoting new environments of learning, but most important growth. The biggest difference for me from high school is the inquisitiveness and enthusiasm. I remember in high-school everyone always complained about this assignment and that test, and actually lost the marvel of learning. In University however you are surrounded by a sea of individuals with the same interests as you, further igniting your passion for math. I just started my second year, and I just keep discovering new benefits of studying math. It depends on what module one takes, but the math still continues to enlighten sides of myself that I forgot I had, for example thinking outside of the box, or getting excited if a math problem sounds crazy or makes absolutely no sense! My advice would be to any scholar coming to university to think about math creatively, observe it around you, talk about it, be brave, ask many questions and most importantly have fun! - Nina Smit
The transition from school Mathematics to University Mathematics is quite challenging. For one, you do not know what to expect and I feel the NSC system fails students who take a deep interest in the STEM field. The mathematics you learn in school is pretty straight forward and answers to questions often follow an obvious algorithm that you can use without even understanding the fundamentals of what you were taught. Mathematics forms an integral part of STEM and I feel schools (or schools in my town) did not emphasize this enough. I know some schools offer Ad Math but the schools in my town didn't which was sad. I feel all schools should offer students the opportunity to challenge themselves with "difficult Math". This would lay a good foundation for students transitioning into university. - Cole Tymothy Paulse
Transitioning from school mathematics to university mathematics can be tricky. The main difference is the way it is taught and examined. In a school mathematics test/exam, you will be expected to answer questions that are similar to the examples you have been shown in class or your homework questions. This is very different in a university setting. Many questions don't look the same as the given examples so you will have to apply the knowledge acquired from the "homework" to solve a problem that is presented in a format that you probably haven't seen. You can't only use the fact that you know the formula and format to solve a university mathematics problem, you need to develop your logical and critical thinking skills and get creative to understand and answer the question. - Refentse Makweya
School mathematics relies heavily on memorization while university mathematics relies on more problem-solving. At school, we are taught a method to solve a specific problem. At university, we are taught certain tools that can be applied to solve various problems in interesting and creative ways. University mathematics courses contain far more work than high school mathematics and learning happens fast. University mathematics assessments often feel more like mathematics olympiads in the sense that the questions are often testing problem-solving abilities over simple memorization. - Anonymous
For my transition...I was really blown out of my mind at how much math in university depended on trigonometric work as well as graphs. I wish the teacher in school could emphasize more on the importance of those topics. It also on the other hand showed me just how much i did not know about maths and to what extent it can be applied. I really do look forward to my journey in maths and all the components I will still learn in the years to come. - Ancois Huysamen
I enjoyed my primary School very much. It should not be surprising that I excelled at mathematics and I was given enough space to attempt other problem-solving methods and also try some harder problems in competitions. In high school, I was given similar freedom to do those things, even if teachers did not know much other mathematics outside the syllabus. I stayed in a traditional high school for two years before being homeschooled. I did the Cambridge syllabus as opposed to CAPS. Cambridge syllabus was significantly more robotic. Every past paper has very similar questions that you can learn how to solve. Also, the memos of these past papers gave marks for some unnecessary steps so memorising solutions on past paper memos was even more vital. In university, I feel a bit more freedom in the methods I can use and I can be confident that as long as I'm clear about what I'm doing, I'll get all the marks. I can also be confident that my lecturer can answer any math-related question I have. - Jayden Thomas Dickson
In short, it was and still is one of the toughest but most rewarding challenges I've ever faced. In my experience, there was a big shift in what we were trying to achieve with mathematics. In high school, I was almost always finding a single answer or a number. The goal was mostly just to find the value of something and use Mathematics as the tool to do so. When I first started University Mathematics I saw quite quickly that most of our time was spent doing something much more useful and amazing. We were using Mathematics to understand and describe things. I started to see and understand how Mathematics was not only a method of problem-solving but also an amazing language of description. A very clear example I could give is my completely different experience with Probability and Statistics. Throughout high school, Statistics was a section I really disliked. It felt boring, repetitive, and pointless. However, when I started with my first-semester module on Probability Theory and Statistics (which thankfully was a compulsory module or I never would have chosen it), it quickly become one of the subjects I most enjoyed. It really challenged how I perceived so many everyday events and interactions. The necessity of going from axioms to proof made the well-established formulas I was shown in high school come to life because I could see with more intuition every term, constant and co-efficient was meaningful and not just conveniently helpful.
All this did come with a much higher requirement for practice, repetition, and the need for failure which was a new experience for me in mathematics. Getting things wrong for the process of learning became a common theme in anything I encountered at university. I realized extremely quickly that battling for hours on a topic and having assessments go terribly on a somewhat frequent basis was a reality I need to accept when it happened and learn from those mistakes because feeling disheartened and frustrated was going to only hurt the process of doing better in future. What made this process less demotivating is also a change in the culture around getting things wrong. In High School getting something wrong felt like a worse fate than trying. Success often seemed the only acceptable outcome. What changed dramatically was that failure became something celebrated as a learning opportunity and was met with countless resources to capitalize on it and the focus from my lecturers wasn't getting me to pass the module but to understand the content and become a better mathematician.
To summarize the transition was a massive one. It has challenged me more than I ever thought it would, but it has given me a viewpoint and appreciation for mathematics that I have never had before. I do wonder how many more of my friends in high school would have a changed perception of mathematics if they could get a taste of what the subject can be in a different environment. Looking back I am also amazed by how much I have progressed throughout the last year and hope that in the future more high school students will be inspired to consider a career in Science and Mathematics. - Chad Robert Davies (see also https://foabma.blogspot.com/2022/02/school-vs-university-mathematics.html)
Mathematical proof is a method of discourse which allows a human being to:
discover new mathematical knowledge,
analyze existing mathematical knowledge,
verify truthfulness of a piece of mathematical knowledge.
The ability to construct a mathematical proof is part of human nature. It is closely related to the ability to form thoughts and reason.
Mathematical knowledge is knowledge of abstract principles about our universe. As such, it requires use of symbols to represent entities
that are inherently abstract. For example, the symbol 2 may represent 2 apples or 2 pears. The number 2 is an abstract entity, since it is not confined to any
of these concrete representations.
Mathematics functions at different levels of
abstraction too. For instance, we may write a symbol, such as n, to represent
any number. In one case we could have n = 2, and in another case we could have n = 3.
This is a second layer of abstraction compared to the layer of each specific number,
such as number 2. Symbols representing abstract entities form basic ingredients of mathematical proof. The most complex parts of mathematical proofs deal with manipulations of these symbols, which sometimes may take an extremely long time. To optimize a proof, it is important to understand its most fundamental components. The aim of these lectures is to provide an exposition of these fundamental components.
Activity.Get Python IDE, if you do not already have one: there are many available, Spyder is recommended (very easy to install). Then, get the file sofia.py, which can be obtained from https://github.com/ZurabJanelidze/sofia. Save sofia.py to the runtime directory of your Python IDE. To test that you have done it correctly, create a separate file named something.py, copy-paste the following code in that file, and run the file with your Python IDE:
These are notes for a colloquium talk to be given at NITheCS.
The Snake Lemma from this fragment of a 1980 film ("It's My Turn", starring Jill Clayburgh and Michael Douglas), along with many other similar theorems in abstract algebra, known to be true for a variety different algebraic settings, can all be established in a unified setting of noetherian forms. This post attempts to give a preliminary step towards a possibly ambitious goal of applying noetherian forms outside abstract mathematics. In this light we propose a variation of this notion, a "noetherian information system", which is intended to be more agile in terms of identifying applications.
General Information Systems
By a network we mean a web of devices and directed binary channels between them ( = a graph in the sense of category theory). An information system over a network consisting of just one device and no channels, is a collection of information clusters, where some clusters may be parts of others.
The picture above describes an example of an information system. The device is a cellphone. A cluster is an approximate GPS location of the cellphone. Six clusters are displayed above, marked by A, B, C, D, E, F. The blue clusters represent GPS locations measured at different times on a given day. The orange ones represent GPS locations measured on another day. In general, the idea is that information clusters in an information system are all possible data that the device is theoretically able to capture/process.
There are two ways to interpret the meaning for a cluster E to be part of a cluster C:
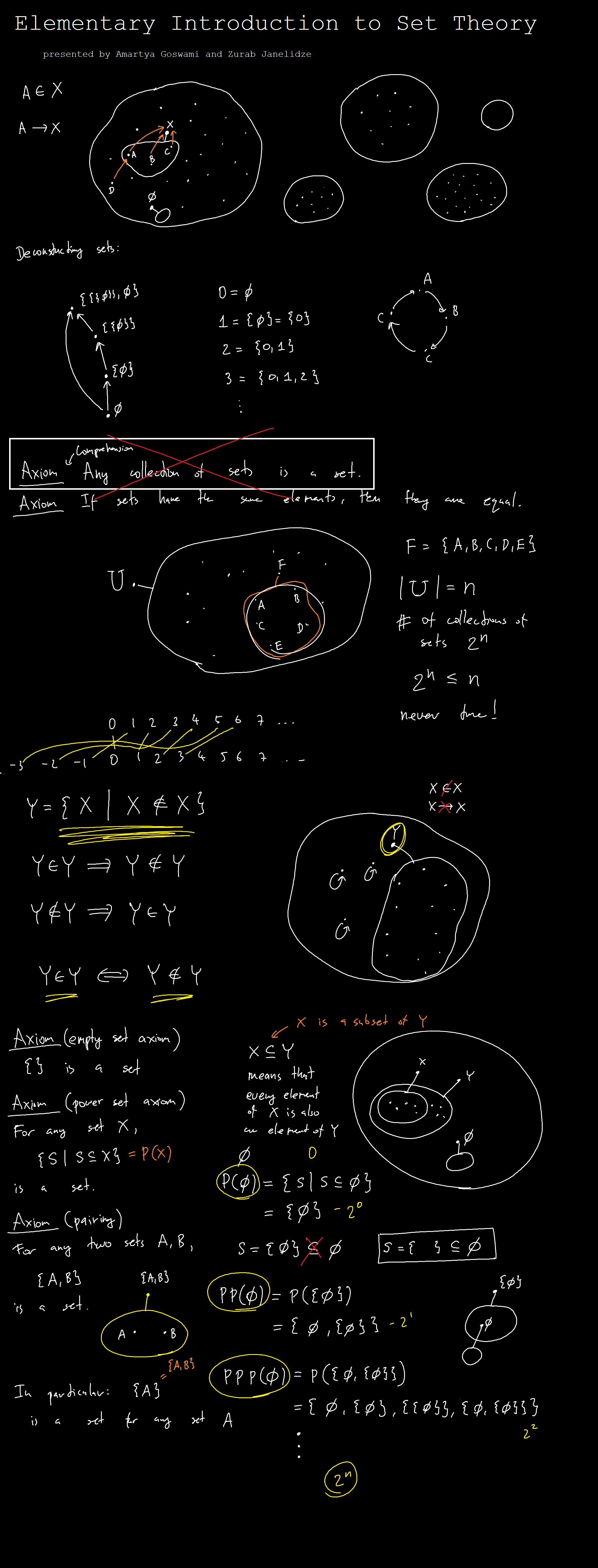
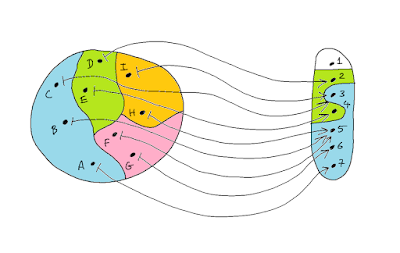
If we think of E as the range of possible locations of the cellphone, then E gives more information about the location of the cellphone than C does.We call this the classical interpretation. In this interpretation, E being part of C gets interpreted as E "implying" C in the sense of classical mathematical logic.
If we think of each possible location as an attribute of the cellphone, then we can interpret E to be a state of the cellphone in which the cellphone has less attributes than in the state C. We call this the quantum interpretation, since with this interpretation, the information cluster E is seen as a state where the cellphone is simultaneously in all locations within the region E.
The general notion of an information cluster is an abstract one, as is the notion of one cluster being part of another. We only require that "is part of" relation between clusters is reflexive, antisymmetric and transitive.
A transmission from one information system to another maps each cluster in one system to a cluster in another system, so that if among two clusters, one is part of another, then a similar relation will hold for the mapped clusters (this property is called monotonicity of transmission). An example of transmission is calculation of distance range to a pinned location, based on the approximate GPS location of the cellphone.
Here the source of transmission is the information system described earlier. The target is an information system where clusters are closed intervals of positive real numbers. The diagram above shows that the cluster C in the first information system will get mapped to the cluster [s,l] in the second information system (where s and l represent lengths of the displayed vectors). In this diagram, L is the pinned location. Monotonicity of this transmission follows from elementary geometry.
In the example above, note that while D is not part of C, it gets mapped to a part of where C maps to. So, in general, transmission does not reflect the "part of" relation between clusters (while it preserves it, by monotonicity).
An information system over a general network consists of information systems over individual devices of the network, where each channel f from a device A to a device B determines a transmission of information from the information system over A to the information system over B. Note that a single transmission itself can be seen as an information system, where the network consists of two devices and one channel between them.
In an information system, given a finite chain of channels
connecting a device U with a device Y, we can consider a transmission from the information system of U to an information system of Y, by composing the transmissions along the chain of channels. We call such transmissions the composite transmissions. This includes the case of an empty chain, i.e., when a chain consists of just one device U and no channels. The resulting composite transmission is then the identity map: it maps every cluster of U to itself. This way, we get a category out of an information system, where objects are devices of the information system and morphisms are composite transmissions. We call it the transmission category. Composition of morphisms in this category is given by further composing composite transmissions. The starting information system then gives rise to a "form" over this category, but we will not go in detail there. Let us just remark that a transmission category can be seen as a subcategory of the category of partially ordered sets. Isomorphisms in the transmission category will be called isotransmissions. These are composite transmissions which admit a two-sided inverse composite transmission.
Henceforth, we we speak of a "transmission" we refer to a "composite transmission", i.e., a morphism in the transmission category.
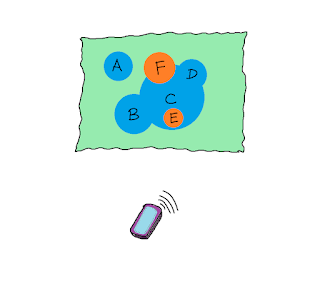
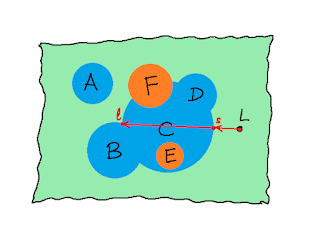
Inputs and Outputs
Define a stash of a transmission to be any cluster that maps to the smallest cluster in the target of the transmission (provided such exists), and define a reach to be any cluster such that there is a cluster in the source mapping to it.
In quantum interpretation, the smallest cluster (when it exists) is given by the least possible attribute set (it must be part of any cluster). Then a stash can be seen as a piece of information that gets concealed (as much as possible) in a transmission. If the smallest cluster is the empty set of attributes, then a stash is a piece of information that does not get transmitted at all.
In classical interpretation, the smallest cluster is a piece of information that logically implies any other piece of information: so it is the logical contradiction (the falsity). In this interpretation, a stash is a piece of information whose transmission results in contradiction. So once again, we may think of this as information that will not get transmitted.
In both classical and quantum interpretations, reach is a piece of received information.
An input is a channel that has the following properties:
Any transmission with the same target as that of the input, whose every reach is a reach of the input, arises as a composite of the input transmission with a transmission to the source of the input.
The input transmission maps clusters injectively (i.e., different clusters do not transmit to the same cluster).
Any cluster that is part of a reach of the input transmission is itself a reach of the input transmission.
An output is a channel that has the following property:
Any transmission with the same source as the output, whose every non-stash is a non-stash of the output, arises as a composite of the output with a transmission from the target of the output.
If the output transmission maps a cluster B to part of a clusters A, and all stashes are part of A, then B is part of A as well.
Any cluster in the target of the output is a reach of the output transmission.
An information system is said to be prenoetherian when the following three conditions hold:
Any transmission decomposes as an output transmission followed by an isotransmission and followed by an input transmission.
For any two inputs there is a third input whose reaches are precisely those clusters which are reaches of both initial inputs.
For any two outputs there is a third output whose stashes are precisely those clusters which are parts of every single cluster containing all stashes of both initial outputs.
Intuitively, the first of these conditions states that any transmission can be replicated through a dedicated transmission and receiving subdevices, between which information transmits without distortion. The second condition assures existence of a receiving subdevice that can capture the same information that two given receiving subdevices both did. The third condition assures existence of a transmission subdevice that can conceal all that the two given transmission subdevices were able to conceal.
Mathematical Examples
Consider vector spaces as devices. Define a channel from a vector space V to a vector space W to be a linear map from V to W. Declare an information cluster to be a subspace of a vector space and declare one cluster to be part of another when the first subspace lies inside the second one. Transmission of subspaces is given by direct image of a subspace under a linear map. The corresponding category of transmissions is equivalent to the category of projective spaces (the quotient of the category of vector spaces, which identifies two linear maps when they act the same way on subspaces). This information system is prenoetherian thanks to the fact that the category of vector spaces is an abelian category. The required decomposition of a transmission is given by decomposition of a linear map as a quotient map, followed by an isomorphism and followed by subspace inclusion. The isomorphism in this decomposition is guaranteed by Noether's First Isomorphism Theorem.
Vector spaces here can be replaced by many other group-like structures. More generally, semi-abelian categories give rise to a prenoetherian information systems similarly to how abelian categories do -- once again, relying on Noether's First Isomorphism Theorem, as well as a few other important "exactness properties".
It has been recently shown that we can even consider a prenoetherian information system where the transmission category is equivalent to the category of sets. Devices in this example are sets. Channels are functions between sets. An information cluster partitions the set into equivalence classes and either distinguishes one of the classes or not. One cluster is part of another, if each equivalence class in the first is a subset of an equivalence class in the second and the distinguished equivalence class (if there is one) in the first cluster is a subset of the distinguished one in the second cluster.
A channel transmission then acts as suggested in the following example.
Distinguished equivalence classes must map to distinguished classes: so if blue is the distinguished class in the source, then in the target, blue must be the distinguished one as well. If, on the other hand, no class is distinguished in the source cluster, then the target cluster will not have a distinguished class either. The required decomposition of functions here is given again by Noether's First Isomorphism Theorem: any function decomposes as a quotient map, followed by a bijection, and followed by a subset inclusion map.
In these examples, every composite transmission is a channel transmission (which is because in each case our starting network was already a category, and transmissions were chosen functorially). When this happens, the decomposition required can by simplified to a decomposition into an output following by an input. This is thanks to the fact that inputs and outputs are stable under composition with channel isotransmissions.
In order to be able to recover all Noether isomorphism theorems in the transmission category of a prenoetherian information system (as well as many other homorphism theorems, such as homological diagram lemmas of homological algebra, for instance), we need to assume that the clusters admit finite suprema and finite infima (i.e., that information systems above each device are lattices in the sense of order theory) and that each transmission is a left adjoint in a Galois connection -- we call such information system a noetherian information system. We consider below a special case of this scenario, where clusters have arbitrary suprema and transmissions preserve them (these correspond to topological functors, whose applications in general topology have been a center of attention for many years in the research group of Professor Guillaume Brümmer from the University of Cape Town).
Topological Information Systems
An information system over a network consisting of just one device and no channels is complete when any number of clusters can be, in the terminology suggested by the quantum interpretation, superposed to form a new cluster. What we mean by "superposition" is nothing other than "join" in the terminology of order theory (so, "disjunction" in the classical interpretation). Superposition of no clusters should also be possible. In this case, the result is the smallest cluster.
None of the information systems considered in the first section of this post are topological.
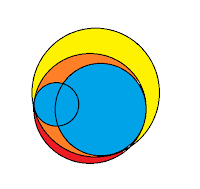
The first information system is not topological since clusters there are always circular regions of a plane. It is impossible to superpose two circular regions into another circular region. Note that a superposition of a set S of clusters is formally defined as a cluster J such that every member of S is part of J and moreover, J is part of any other cluster K that has the same property (i.e., that every member of S is part of K). So superposition of two disks should be a disk which contains both, but which is contained in any other disk containing both. Such disk does not exist unless one of the two disks contains the other: on the illustration below, an attempt to superpose two blue disks must produce a disk that wholly lies both in the yellow disk and the red disk, i.e., that lies in the orange region, while at the same time contains both blue disks -- this is not possible.
Although non-zero finitely many closed intervals can be superposed, infinitely many, in general, cannot be superposed.
In both cases, empty superposition is not possible.
A transmission is said to be continuous when transmission of information preserves superposition of clusters. In particular, when:
the smallest cluster is transmitted to the smallest cluster, and
superposing clusters in the source information system and then transmitting the resulting cluster, is the same as first transmitting the initial clusters and then superposing them in the target information system.
A general information system is topological when all information systems over individual devices are complete and all transmissions are continuous.
It is not difficult to amend our example(s) considered in the first section of this post to get topological information systems. For approximate GPS locations, we can allow any planar region to be a cluster and not just a circular one. For distance ranges, we could allow any set of numbers to be a cluster. The transmission of measuring distance ranges from a pinned location will then be continuous too for general mathematical reasons.
In a topological information system, every transmission can be reversed: the reverse of a transmission f is given by mapping a cluster D in the target of f to the superposition of all clusters that by f are mapped to parts of D. Writing f S for the result of mapping S by f, and writing Df for the result of mapping D by the referse of f, we get the following impressive law:
The middle symbol here is the symbol for logical equivalence. The inequality expresses that the cluster on its right side is part of the cluster on its left side. This is the familiar law of Galois connection in mathematics (written out in a slightly untraditional manner). Intuitively, the reverse transmission recovers largest possible cluster that can get transmitted into a given one.
In our example, reverse transmission of a distance range will result in the following region, which is the region of all locations that are in that distance range from the given location.
The seemingly simple law above has a number of useful mathematical consequences. We describe some of these below:
Reverse transmission is monotone and it preserves meets of clusters (a meet of a set of clusters is defined as the largest cluster that is part of each cluster).
Transmission followed by reverse transmission results in expansion of the cluster.
Reverse transmission followed by transmission results in shrinking of the cluster.
Transmission, then reverse transmission, and then transmission again, results in the same cluster as by initial transmission. There is a similar property starting with reverse transmission in the place of transmission.
Concluding Remarks
The notion of a noetherian information system from this post is an adaptation of the notion of a noetherian form from
A. Goswami and Z. Janelidze, Duality in non-abelian algebra IV. Duality for groups and a universal isomorphism theorem, Advances in Mathematics 349, 2019, 781–812.
Related references, and especially those which led to the development of this concept, can be found in the article above. In particular, it contains the following reference to the paper of Emmy Noether where her isomorphism theorems were first established:
E. Noether, Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern,
Mathematische Annalen 96 (1927), 26–61.
In the following paper, Saunders Mac Lane, suggested that there should be a unified categorical approached to isomorphism and other such theorems based on duality:
S. Mac Lane, Duality for groups, Bull. Am. Math. Soc. 56, 1950, 485–516.
Noetherian forms provide such approach. The example dealing with the category of sets can be generalized to any topos (joint work in progress with Francois van Niekerk). Keeping in mind that the notion of a topos is a notion of a mathematical universe, we see how noetherian information systems have a wide reach in abstract mathematics. This makes one wonder whether they can be found outside of mathematics as well? In particular:
Is there a useful real-life interpretation of a noetherian information system?
If yes, does it lead to the ability to usefully model real-life information systems as noetherian information systems?
In particular, are there any applications in machine learning or data science?
Or, is it perhaps possible to use noetherian information systems to usefully model function of a living organism, or maybe, cognitive function of a human being?
Does the category of Hilbert spaces, which is neither an abelian nor a semi-abelian category, but which plays an important role in quantum mechanics, have a noetherian form?
Can the physical universe be modelled as a noetherian information system?
