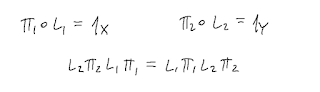The Merriam-Webster Dictionary defines the word "monotony" as "tedious sameness". For a creative soul, monotony is on par with torture. This piece conveys the struggles of the soul that has been trapped in monotony and is looking for ways to break free from it. The video shows a man performing various free style dance moves as an expression of the struggles. Behind him is a wall on which, in the first part of the video, projects a movie of clouds moving through the sky. This is a symbolism of one's creative aspirations before one becomes a prisoner of monotony. In the second part of the video, the projection changes to showing the dancer in action, from multiple angles. This symbolizes that after a while of monotony, the aspirations dissolve into excessive awareness of one's own self. At this stage, an illusion of having broken free from monotony may arise, which is symbolized by the scene with the chair. The chair is the illusion of freedom, illustrated by the dancer performing various dance moves over and around the chair. During the scene with the chair, the music is cheerful. This scene transitions into a scene leading to the finale, where the chair is gone and the mood of the music drops low signifying the sad realization that the feeling of having broken free from monotony was only an illusion. Right at the very end, the scene shows the dancer up close. A moment after the music has stopped, the dancer abruptly turns his head around as part of what seems to be another dance move, which ends the video. It leaves the viewer uncertain whether monotony has been overcome or not; the intention here is to urge the viewer to contemplate on their own monotony and ask the question whether it has been overcome or not?
A Gap in Mathematics Education
The process of creation of mathematics has the following hierarchically dependent components:
- Coming up with a concept.
- Coming up with a question dealing with a relationship between concepts (this includes formulating a hypothesis, as well as finding an example or a counterexample of a concept/phenomenon).
- Answering a question dealing with a relationship between concepts (this includes proving theorems as well as solving problems without being given the recipe for solution).
- Applying the answer to a question dealing with a relationship between concepts to answer another such question (this includes solving problems by applying a given recipe for solution).
Modern mathematics education (both at the school and at the university levels) focuses mainly on the last two points. What is regarded as a low quality mathematics education would focus only on the last point. For a more whole mathematics education, the first two points must receive as much attention as the last two points do.
It is not difficult to implement the first two points in the practice of mathematics teaching. Here is an example of the structure of a class that focuses on the second and the third points:
- The teacher proposes one or two concepts that the pupils are familiar with (perhaps, by taking suggestions from the class).
- The teacher then asks the pupils to explain the concepts, helping the pupils in the explanation, when necessary.
- Then, the teachers asks the pupils to think of a question that would combine the named concepts. The teacher helps in this process.
- After this, the teacher and the pupils engage in answering the question together.
- If the question is too hard to answer, it should be concretized to a simpler question. If the question is too easy to answer, it should be abstracted to a more difficult question.
Concepts arise in mathematics as a necessity to help one express a general phenomenon. Incorporation of the first point in a classroom can be achieved by explaining this necessity for the concepts that the pupils are already familiar with, or by taking pupils on a journey that would help them identify such a necessity and will result in (re)discovering a mathematical concept. Teaching concepts by first showing examples and then asking the pupil to develop a concept that fits those examples is another, perhaps simpler, way. The activities which ask a pupil to identify a pattern in a sequence of numbers or figures is in some sense of this type. However, these activities are sold as activities that fall under the third point, as the pupil is being convinced that the question must have one definite answer.
Metaphysics of Human Function based on a Mathematical Structure
work in progress
I propose here a theory of human function, which I have been developing based on introspection. In this theory, human function is represented in terms of exchange of information of four agents, which I call the spirit, the mind, the soul and the body. Although these are surely familiar terms, having a variety of scientific, pseudo-scientific, religious, philosophical and other usage, I do not assume any insight derived from such usage. The essence of each of these agents will be revealed through the roles that they play in human function. Matching of this essence with any of the existing definitions of these entities is unintentional and may well be coincidental.
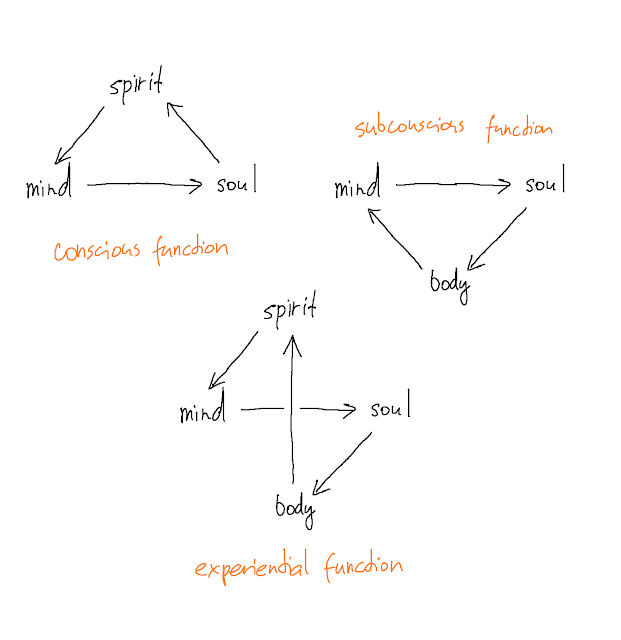
The four agents are organizes in the following directed graph:
Postulate 1. Human function is marked by internal information processing within each of the four agents as well as exchange of information along the arrows of HFS.
Postulate 2. When a human being is engaged in a particular activity, information flows between the agents in consistent cyclic patterns. Change of activity may change these patterns.
Postulate 3. These cyclic patterns are made of three fundamental ones - the three cycles of HFS.
The cycles referred to in Postulate 3 are:
The arrow going out of Spirit is the channel through which our conscious impacts human function. We call information flowing along this arrow Will. The rest of the arrows have names too: subconscious perception (for Body to Mind), abstraction (for Mind to Soul), concretization (for Soul to Body).
Noetherian Forms
Link to a plenary talk on noetherian forms at a BRICS conference (2021): slides of the talk, recording of the talk.
Link to a talk on noetherian forms at the PALS seminar (2020): written summary, recording of the talk.
Noetherian forms are mathematical structures defined by self-dual axioms, that include all lattices, Janelidze-Marki-Tholen semi-abelian categories and Grandis exact categories. They can be seen as a realization of Saunders Mac Lane's hypothesis from his 1950 paper on Duality for Groups that self-dual axioms can be found to treat isomorphism theorems for non-abelian groups, as this is realized for abelian groups with the notion of an abelian category. Abelian categories are actually given by the overlap of semi-abelian and exact categories.
The term "noetherian" refers to the fact that these forms can seen as a fulfilment of Emmy Noether's program to "disregard the elements and operations in algebraic structures in favor of selected subsets, linked to homomorphisms between structures by the homomorphism and isomorphism theorems" - quote from Colin Maclarty's article.
See this list for relevant papers in this research area.
Work in progress and current conjectures / open questions regarding noetherian forms:
- Noetherian forms found for the category of sets - a paper on this is in preparation. Conjecture: these forms are present already for an arbitrary topos.
- The category of Hilbert spaces and continuous linear maps is an additive category, but not an abelian category. Conjecture: it nevertheless admits a noetherian form. Question: if there is indeed such noetherian form, is it of any use for quantum mechanics / quantum field theory?
Abstract Structures in Mathematics and Music
These are notes for my online discussion with Georgian Student Parliament on Tuesday 7 December, 2021, organized by Nina Tsatsanashvili. All photos in this post are from Wikipedia.
If you look up the word "structure" on the Google Dictionary, you will find the following definition: the arrangement of and relations between the parts or elements of something complex. When the "parts or elements" are subject to specific interpretation, we have at hand an "abstract structure". For example, consider a painting, which can be seen as an arrangement of colors. For instance, Leonardo da Vinci's Mona Lisa:
In this sense, abstract mathematics is similar to composition in music: in both cases one builds structures that are inherently abstract. The analogy goes further: a musical performer can be compared to an engineer, for instance, who produces concrete structures by means of concrete interpretations of the abstract mathematical structures.
As an example of a form of abstract structure in mathematics, consider the following diagram:
Similarly, in a single musical composition, there is one (or several) main forms of musical structure, whose different manifestations are being explored, along with their interrelations, in the composition. What is the main form of musical structure in Für Elise?
A surprising story of how a computer was taught to prove some theorems in finitely complete categories
Notes for the talk given at the 2021 Congress of South African Mathematical Society on 29 November.
Note that we can disregard the RHS of the equalities in the system if we agree to always use the subscript "0" for the variable there.
Such notion can be produced for every matrix M of integers, of arbitrary dimensions. The number of rows of the matrix determines the arity of the "internal binary relation" for which "strict M-closedness" will be defined.
We leave it as an exercise to find the Mal'tsev and majority matrices in this diagram (note that matrix properties are invariant under permutation of columns in the representing matrix).
1. Finitely complete categories
A finitely complete category is a category that has finite products and equalizers (and hence, all finite limits). Not every category is finitely complete, but most categories of mathematical structures are.
There is a representation theorem for finitely complete categories (Yoneda embedding), which allows to present any category as a full subcategory of a (larger) category of presheaves of sets, which is closed under all limits that exist in the category. This means that a lot of times, proving a theorem in a finitely complete category involving finite limits, reduces to proving the same theorem in the category of sets.
For instance, the fact that the product of objects is commutative, up to a canonical isomorphism, can be deduced from the fact that the same is true for the cartesian product of sets. Or, the fact that the composite of two monomorphisms is a monomorphism can be deduced from the fact that composite of two injective functions is injective.
2. Mal'tsev conditions
What would we want to prove in a finitely complete category that is not easily true in the category of sets?
A lot of Mal'tsev conditions encountered in universal algebra can be reformulated as properties expressible in any category. Historically first Mal'tsev condition, stating that there is a ternary term "p" satisfying the following identities, is such.
The "x"-s here represent variables of the algebraic theory of a variety of universal algebras. The condition above states that it is possible to express an operator "p" using basic operators of the theory, such that the identities become theorems of the algebraic theory (once the "x"-s are universally quantified); equivalently, these identities hold in every universal algebra of the variety.
Such term "p" can be found in varieties of group-like structures, where we can set:
An abstract finitely complete category, however, possesses no algebraic theory and so it becomes impossible to talk about the term "p" (at least, not quite, see this paper from 2008, by D. Bourn and myself). Nevertheless, it is possible to reformulate the property of the existence of "p" as a property of the category of algebras in the variety. And there are many other Mal'tsev conditions which can be so reformulated!
3. Matrix properties
What we may be interested in, then, is when does one such reformulated Mal'tsev condition imply another, in any finitely complete category?
The reformulated Mal'tsev conditions that we consider can be described by matrices of integers that appear as subscripts of the corresponding system of term identities. For instance, in the case of the system considered above, the matrix would be
To describe the corresponding condition on a category, we first need the following notion:
The condition on a finitely complete category corresponding to a matrix M states that every internal relation in it (of suitable arity) is strictly M-closed. In the case of the matrix M considered above, this is the familiar property that defines a Mal'tsev category as a finitely complete category in which every internal relation is difunctional, considered here:
The corresponding term can be found in varieties of lattice-like structures, where
In attempting to show that protoarithmetical categories in the sense of D. Bourn are not the same as Mal'tsev majority categories, he discovered that the duals of the categories of relations (on sets) are able to detect implications of matrix properties (see this paper of his). This leads to formulating an algorithm, that we implemented on a computer, for deciding implications of matrix properties.
The first row of this table states the theorem. The purple matrix is the Mal'tsev matrix. The orange matrix is the majority matrix. The blue matrix is the matrix corresponding to the property of arithmeticity. The theorem is thus that the first two matrix properties together imply the third. According to our algorithm, the following procedure allows to confirm this implication.
To prove that one matrix property implies another in any finitely complete category, we would have to begin with an internal relation R for which we want to establish a property N, and build from R, using finite limits, another internal relation S for which we would apply a property M to conclude that R has the property N. Thanks to the representation theorem above, this reduces to doing the same inside the category of sets. However, it does not really simplify the task: finding the construction of a suitable relation S to get the desired property of R may be tricky.
4. Michael's work
A surprising insight comes from Michael Hoefnagel's work on "majority categories". These are categories defined by the matrix
The story of how exactly one arrives to the algorithm is an interesting one in its own right. It actually builds on ideas contained in this paper of Thomas Weighill, which is another interesting story that comes out of an observation of how the Mal'tsev property (corresponding to the first matrix considered above) relates to a separation axiom in topology.
5. The algorithm
Here we cut short all of these interesting stories and instead, present the algorithm directly, on a concrete example.
As we will explain below, the following table gives a proof of the fact that a Mal'tsev majority category has the matrix property of "arithmetical varieties".
We want to introduce new columns to the blue matrix until we get a column of 0's. To do that, consider the orange matrix in the second row. Each row in this matrix is obtained from the orange matrix in the first row by renaming its entries (the renaming rule may be different across different rows). The corresponding renaming of entries in the invisible column of 0's of the orange matrix in the first row, results in the blue column in the second row. Each row of the blue column thus shows to what was 0 renamed in the corresponding row of the orange matrix (in the second row of the table). Furthermore, every column of the orange matrix in the second row of the table must be a column of the blue matrix in the first table. Similarly, the in the third row of the table we finally obtain the blue column of 0's. This time, we rely on the purple matrix rather than the orange one. Just like the orange one, that purple matrix has every row obtained from a row of the purple matrix in the first row of the table by renaming of its entries, while every column of the purple matrix is one of the previous blue columns (including the one obtained in the previous step).
That the successful execution of the procedure above can confirm the theorem was already known, at least implicitly, from this paper of mine, which is one of the first two papers on matrix properties. What is new is that we now know that a theorem stating implication of matrix properties will be true if and only if it can be established using the algorithm. Thus, in the language of mathematical logic, we had soundness and now we have established completeness.
6. Computer enters the scene
Execution of the algorithm above may not be easy at all. Although the process is always finite, there may be a significant amount of steps we need to take, before we reach the destination. By hand, this task may take a very long time. In fact, it may take a long time even using a computer. Nevertheless, the computer can do better. The following computer-generated image shows all implications between equivalence classes of matrix properties given by "binary matrices" having four rows and up to seven columns, where black spots represent entry 1 and white ones represent entry 0:
Interestingly, the poset above (which grows from left to right) appears to have the smallest element -- the left-most matrix. This matrix is in fact the one corresponding to the property of arithmeticity. As Emil van der Walt (grandson of Andries van der Walt) proved in his first year of undergraduate studies, this matrix property implies every other binary matrix property. It has been furthermore shown that every binary matrix property either implies the Mal'tsev one, or is implied by the majority property.
7. Concluding remarks
Let me conclude by adding to the title: not only was a computer taught to prove some theorems in finitely complete categories, but the computer also helped us to identify new theorems that we, humans, were able to prove (and which would be impossible for the computer to prove using the algorithm, since they deal with an infinite number of matrices).
The results described in this talk are taken from two recent papers, the first by Michael Hoefnagel, Pierre-Alain Jacqmin and myself, and the second, by the three of us and Emil van der Walt. The work on these papers is complete and links to them will be placed here once they are published. You can see the arXiv preprint of one of them (note however that a slightly revised version of this preprint is still to be posted). The work on both of these papers was carried out in 2020-2021, and started with a visit of Pierre-Alain Jacqmin to Stellenbosch in January 2020.
Matrix Properties
Matrix properties are a particular type of exactness properties that can be seen as category-theoretic analogues of linear Mal'tsev conditions in Universal Algebra. See this list for relevant papers in this research area.
The study of matrix properties led to the theory of "approximate operations" developed jointly with Dominique Bourn, and a general theory of exactness properties developed jointly with Pierre-Alain Jacqmin.
Work in progress on matrix properties:
- Open problem on finding an algorithm for implication of basic matrix properties solved - see the working version of the preprint.
- Even for binary matrices, the preorder of implications is quite complex. Some new results on this appear in this work in progress.
- Python implementation of the algorithm for deducing implication of (basic) matrix properties can be found here. The program needs to be improved in some future.
2021 Academic Activities
Summary
- Elected as the President of the South African Mathematical Society.
- Papers on exactness properties published in Journal of Algebra and Advances in Mathematics.
- Invited to give a plenary talk at the BRICS Mathematics Conference.
- Secured funding for a national research programme in mathematics.
- First computer implementation of the SOFiA proof system developed.
- Supervised four postgraduate students (two PhD and two MSc).
- Two papers on matrix properties submitted.
- Served as the mathematical sciences programme coordinator and on a university research committee.
- Taught and/or convened two semester modules and two year modules.
- Progress made on existing and new research projects and delivered talks on those.
- Carried out duties in the role as mathematical sciences programme coordinator and member of a university research committee.
- Carried out refereeing and editorial duties (not listed below).
November-December 2021
- Finalized marks for Foundations of Abstract Mathematics I, II and an honors module in Logic.
- Resumed research on a noetherian form of sets.
- The binary matrix properties paper submitted for publication (corresponding author: M. Hoefnagel) - see the submitted version of the paper here.
- The revised version of the paper on matrix taxonomy re-submitted for publication (corresponding author: M. Hoefnagel) - see the new version here.
- Talk given at SAMS Congress on the matrix project - see the write-up of the talk here.
- At the SAMS AGM held during the congress, I was appointed to serve on the SAMS Council as the President of the South African Mathematical Society for 2022-2023.
- Plenary talk given at the 4th BRICS Mathematics Conference on noetherian forms (slides, recording). This talk was given jointly with Amartya Goswami.
- Funding awarded for the NITheCS research programme in Mathematics, entitled "Space-like mathematical structures and related topics in algebra, logic and computation", which was expanded to include 20 mathematicians in South Africa.
- Mathematical Sciences Programme tasks continued.
September-October 2021
- Paper published: linear exactness properties in Journal of Algebra. See the paper on the journal's website here.
- Some progress made on the SOFiA project, including implementation of an intuitive command-line proof building interface for sofia.py. Used this tool in the delivery of the Foundations of Abstract Mathematics I seminar in the fourth term.
- The binary matrix properties paper finalized from my side.
- Worked on the revision of the matrix taxonomy paper. Revision in progress can be found here.
- Together with Amartya Goswami, gave a NITheCS mini-school (October 2021) on Elementary Introduction to Category Theory. See this blog for the write-up and links to video-recordings of lectures.
- Talk given at SIC on forms vs monoidal categories. See the write-up and the recording of the talk here. See the recordings of all talks here.
- Examiners nominated for the MSc Thesis of Paul Hugo, to be finalized by the end of the year.
- Developed a NITheCS national programme in Mathematics for 2022, under collaboration with Amartya Goswami, Partha Pratim Ghosh and Yorick Hardy.
July-August 2021
- Further progress made on the binary matrix properties paper.
- Started writing a book in abstract algebra jointly with Amartya Goswami. You can follow the progress here.
- Started work on some tasks related to the Mathematical Sciences Programme.
- Teaching Foundations of Abstract Mathematics II in the third term and honor module in Logic in the second semester.
- Started sketching ideas for a NITheCS national programme in Mathematics for 2022.
May-June 2021
- The paper on linear exactness properties, joint work with Pierre-Alain Jacqmin, was accepted for publication in Journal of Algebra (it is scheduled for publication in October 2021 - follow the link).
- Started (co-)supervision of PhD studies of Brandon Laing on SOFiA.
- Started supervision of PhD studies of Ineke van der Berg on categorical algebra of algebraic logic.
- Started a new research project on applications of forms to physics.
- Continued with the teaching of Engineering Mathematics 214 and Set Theory and Topology.
- Busy with marking of Foundations of Abstract Mathematics I first term seminar final assignments.
March-April 2021
- Started work on matches of digraphs: pioneering joint work with Francois van Niekerk and Jade Viljoen (research grew out from her honors project).
- Started work on binary matrix properties: joint work with Michael Hoefnagel, Pierre-Alain Jacqmin and Emil van der Walt (undergraduate student) on the structure of the poset of matrix properties. The project grew out from Emil solving problems that Michael and I suggested to him in the fall of 2021, which naturally evolved from a joint work with Michael and Pierre-Alain.
- Made some progress with SOFiA: joint work with Louise Beyers, Gregor Feierabend and Brandon Laing. First python implementation of the SOFiA proof system produced. As a result, its deduction rules were refined.
- Started supervision of MSc studies of Daniella Moore on categorical aspects of near-vector spaces (cosupervised by Karin Howell).
- Teaching Engineering Mathematics 214 (together with Liam Baker, Ronalda Benjamin, and Michael Hoefnagel) in the first semester and giving a Foundations of Abstract Mathematics I seminar in Mathematical Reasoning in the first term. Also teaching an honors module, Set Theory and Topology, in the first semester.
January-February 2021
- The paper on stability of exactness properties under pro-completion, a 7 year old joint work with Pierre-Alain Jacqmin, was published in Advances in Mathematics.
- The paper on matrix taxonomy has been submitted for publication.
- Revisited research on a noetherian form of sets: together with Francois van Niekerk, we are elaborating the proof of our recent theorem that the category of sets provides a model for the self-dual axiomatic setup for homomorphism theorems proposed in my publication no. 35. Significant progress was made with the corresponding paper, but it still needs to more work.
- Serving on the Subcommittee B of the Research Committee of Stellenbosch University for 2021, as well as on the Programme Committee of the Faculty of Science.
Forms vs monoidal categories
Below is a summary of the talk given at the Séminaire Itinérant de Catégories (8 October 2021), prepared before the talk. The talk is mainly based on Zurab Janelidze's joint work in progress with Francois van Niekerk, as well as his earlier work on forms with former collaborators.
The talk assumes that the listener is familiar with basic ideas and concepts of category theory found in Categories for the Working Mathematician by Saunders Mac Lane (in particular, Chapters I, VII and VIII), as well as with the notions of factorization system and Grothendieck fibration.
1. Biproducts, products, sums and monoidal categories
The goal of this talk is to explain the following diagram:
Most categories are not linear. Matching of products and sums is a rare phenomenon. So instead of their matching, one looks for a common generalization of these two constructions, especially that there are many other interesting ways of combining objects which one would also want to include under the generalization. The classical example of a construction of combining objects which is neither a product nor a sum is the construction of a tensor product of two abelian groups. A common generalization of these constructions is of course the notion of a monoidal category.
We have thus far described the fragment of the above diagram enclosed in the region shown below:
2. Algebraic vs geometric nature of a category
We will now describe the fragment of the initial diagram enclosed in the region shown below:
3. Short exact sequences, subobjects, quotients, and forms
Linearity is an important ingredient of the notion of an abelian category. Another important ingredient is exactness: that every morphism decomposes as a cokernel followed by a kernel. The following result is from "Duality in non-abelian algebra II" by Z. Janelidze and T. Weighill (Journal of Homotopy and Related Structures, 2016):
- A Grandis exact category is a category equipped with an ideal of null morphisms in the sense of C. Ehresmann, such that every morphism admits a decomposition into a cokernel followed by a kernel, relative to the ideal. In the pointed case, this becomes the notion of a Puppe-Mitchell exact category: a pointed category where every morphism decomposes as a cokernel followed by a kernel (both in the usual sense of a pointed category).
- An Isbell bicategory is a category equipped with a proper factorization system. The corresponding "form of quotients" is the fibration of quotients and the "form of subobjects" is the opfibration of subobjects.
Specializing the result above to a pointed category equipped with a proper factorization system given by a class "E" of epimorphisms and class "M" of monomorphisms, we get the following
Theorem: Such a category is exact (i.e., every morphism decomposes as a cokernel followed by a kernel) if and only if the fibration of "E"-quotients is isomorphic to the opfibration of "M"-subobjects.
This theorem is analogous to the fact that a pointed category is linear if and only if it has binary sums and products such that the monoidal structure of sum is isomorphic to the monoidal structure of product. In this analogy, the notion of subobject corresponds to the notion of product and the notion of quotient corresponds to the notion of sum. What corresponds to a monoidal structure is a form, by which we simply mean a faithful functor whose fibres are posets. Both, fibrations of quotients and opfibrations of subobjects are forms. A form equips every object of the category with a poset (the fibre at that object), so in view of the previous discussion about algebraic vs geometric nature of a category, a form can be seen as a geometric enforcement of the notion of a category. There are two canonical types of forms, given by subobject forms and quotient forms, just like there are two canonical types of monoidal structures given by products and sums. Their coincidence, in the context of a pointed category equipped with a proper factorization system, gives, by the above theorem, a characterization of exact categories. On the monoidal side, what corresponds to requiring the existence of a proper factorization is the requirement of the existence of all finite products and sums.
To complete the analogy between the monoidal vs formal situations, we need to answer the following questions:
Question 1. What is geometric/formal analogue of tensor product as a third type of monoidal structure, different from product and sum, but nevertheless an important example of a monoidal structure?
Question 2. What is geometric/formal analogue of the notion of a biproduct?
We leave answering the first question to the end of the talk and answer now the first question. A biproduct is, loosely speaking, something that is both a product and a sum, plus these two must satisfy compatibility conditions. Thus we want something that is both a subobject and a quotient with some compatibility conditions. The answer is: a short exact sequence, i.e., a sequence of morphisms
where the first is a kernel of the second and the second is a cokernel of the first. A linear category can be thought of as a pointed category having sufficiently many biproducts, where "sufficiently many" means that any two objects can be completed to a single biproduct diagram. With some loose analogy, here, an exact category is a pointed category having sufficiently many short exact sequences, where "sufficiently many" means, this time, that any single morphism can be completed to a commutative diagram with two short exact sequences:
4. A Noetherian Form over the Category of Sets
A noetherian form is a form satisfying the axioms given in the paper "Duality in non-abelian algebra IV" by A. Goswami and Z. Janelidze (Advances in Mathematics, 2019). These axioms are self-dual in the sense that a form satisfies them if and only if the dual form (i.e., the dual functor) satisfies them. The axioms allow to establish homomorphism theorems for group-like structures, such as the isomorphism theorems and homological diagram lemmas.
The form of subobjects/quotients of an exact category is noetherian. The form of subobjects of a category having finite limits and colimits is noetherian if and only if it is a semi-abelian category in the sense of G. Janelidze, L. Márki, and W. Tholen (J. Pure Appl. Algebra, 2002). Although neither the category of sets, nor its dual, is a semi-abelian category, it still has a noetherian form. This form is neither a subobject form and nor it is a quotient form. Under this form, the fibre of a set is given by the poset of ordered pairs consisting of an equivalence relation and a subset that is a union of equivalence classes. This form is the (an) answer to Question 1. A thorough analysis of this form is being written up in a joint work of Zurab Janelidze and Francois van Niekerk, which is based on the results given in the PhD Thesis of the second named author.
5. Contrasting Features of the Monoid-Form Analogy
As demonstrated above, there is a striking analogy between the monoidal/formal roots of the notion of an abelian category. This analogy has some interesting contrasting features too:
- A monoidal structure is an internal monoid in the 2-category of categories. A form is not an internal poset in the 2-category of categories.
- Products and sums, once they exist, are unique (up to isomorphism). A category may have several non-isomorphic proper factorization systems.
- Isomorphism between the monoidal structure of product and the monoidal structure of sum forces the category to be pointed. Exact categories need not be pointed categories.
The middle point above could perhaps be remedied by relaxing the notion of a monoidal structure of sum (and accordingly, the dual notion of a monoidal structure of product), replacing it with sum structure in the sense of Z. Janelidze (Cover Relations on Categories, Applied Categorical Structures, 2009): a monoidal structure where the monoidal unit is an initial object and the resulting canonical morphisms into the tensor,
6. Conclusion
An intriguing analogy between the monoidal roots and the formal roots of the notion of an abelian category leads to a new notion of a "bisum structure", which under this analogy presents itself as the counterpart of a Grandis exact structure. Combining these two notions may give an interesting generalization of the notion of an abelian category, not considered yet in the literature. Relaxing a Grandis exact structure to a noetherian form, these ideas will come close to the ideas of Francois van Niekerk developed in "Biproducts and commutators for noetherian forms" (Theory and Applications of Categories, 2019): there he defines a biproduct in the context of a noetherian form, which is an example of our bisum structure.
Lectures
- Calculus (notes in progress in Real Variable Calculus)
- NITheCS Mini-School on Elementary Introduction to Category Theory, a series of lectures for the October Mini-School at the South African Mini-School in Theoretical and Computational Sciences, given jointly with Amartya Goswami
- Abstract Algebra for the Future Mathematician, a book in progress jointly with Amartya Goswami
- The Caravan this is an introductory book in progress on foundations of abstract mathematics.
- My inaugural lecture publication and the lecture.
- See the mathematics playlist of my youtube channel for my video lectures.
- Cardinal Arithmetic (Cantor’s theory of cardinality for Grothendieck-type universes)
- Morphisms of finite spaces (introduction to the basic ideas of category theory via topology and combinatorics)
- Posets and connections (introduction to Galois connections)
- Homomorphisms of monoids (includes products, sums and quotients of monoids)
- Universal algebra (Birkhoff’s variety theorem and some Mal’tsev conditions)
- Abstract logic (work in progress)
- Categories (extremely basic introduction to categories)
- Universal properties (a prelude)
- Regular categories (basics)
- An abelian exploration of diagram lemmas (notes for the lectures delivered under the Erasmus+ program in 2018 at the University of Lovain-la-Neuve)
- Calculus of exact sequences (notes for the lectures delivered under the Erasmus+ program in 2017 at the University of Lovain-la-Neuve)
- Written lecture # 100 on Laplace transform
- Written lecture # 101 on Laplace transform (second part)
- Written lecture # 102 on basic constructions with sets
- #103 on real vector spaces
- #104 on equivalence relations
- #105 types of continuous functions
- #106 constructions with topologies
- #108 open interval topology
- #109 linear maps and the eigenvalue problem
- #110 homeomorphisms
- Incidence relation (a small fragment of Euclid-Hilbert axiomatic geometry)
- Universes of Sets (a first course on axiomatic set theory based on the work of Zermelo)
- Relations (includes functions as defined by Dedekind, equivalence relations and partial orders)
- Natural Arithmetic (axiomatic development of the natural number system within set theory, following Dedekind and Peano)
- #111 the concept of unit fraction